Learn – Geometry – Circles

Chords and subtended angles

Exercises

Problem set

  1. Prove that congruent chords of a circle subtend congruent angles at the center.
  2. Prove that chords of a circle that subtend congruent angles at the center are congruent.
  3. Prove that the perpendicular from the center of a circle onto a chord bisects the chord.
  4. Prove that the line drawn through the center of a circle bisecting a chord is perpendicular to the chord.
  5. Prove that there is one and only one circle that passes through three non-collinear points.

Problem set

  1. Prove that two congruent chords of a circle are equidistant from the center.
  2. Prove that two chords of a circle equidistant from the center are congruent.
  3. Prove that angle in a semicircle is a right angle.
  4. Prove that the all inscribed angles subtended by a chord on the same side of the chord are congruent.
  5. Prove that the sum of each pair of opposite angles of a cyclic quadrilateral is 180^\circ.
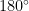  6. Prove that if the sum of a pair of opposite angles of a quadrilateral equals 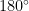180^\circ, then the quadrilateral is cyclic.
  7. Prove that a parallelogram cannot be cyclic unless it is a rectangle.

Problem set

  1. PQRS is a cyclic quadrilateral. If \angle SPR = 70^\circ and \angle SQP = 30^\circ, find the measure of \angle PSR.

Areas and perimeters

Exercises

Problem set

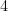  1. The subtended angle of a sector is 30^\circ. The radius of the sector is 4 units. What are the area and perimeter of the sector?
  2. Two sectors are cut off in a circle such that the angle subtended in one sector is twice that in the other sector.
    1. What is the ratio between the arc lengths of the sectors?
    2. What is the ratio between the areas of the sectors?
  3. Two sectors have the same subtended angles. Radius of one sector is twice the radius of the second sector.
    1. What is the ratio between the arc lengths of the sectors?
    2. What is the ratio between the areas of the sectors?
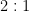  4. Two sectors whose radii are in the ratio 2:1 have the same area.
    1. What is the ratio between the arc lengths of the sectors?
    2. What is the ratio between the subtended angles of the sectors?
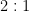  5. Two sectors whose radii are in the ratio 2:1 have the same arc lengths.
    1. What is the ratio between the areas of the sectors?
    2. What is the ratio between the subtended angles of the sectors?

Problem set

  1. Radius of a regular hexagon is twice that of the radius of another regular hexagon. What is the ratio between their areas?
  2. Perimeter of a regular octagon is a third that of the perimeter of another regular octagon. What is the ratio between their areas?
  3. Area of a regular pentagon is sixteen times the area of another regular pentagon. What is the ratio between their perimeters?

Problem set

  1. In the following figure, determine the area and perimeter of the shaded portion.
  2. In the following figure, determine the area and perimeter of the shaded portion.
  3. In the following figure, determine the area and perimeter of the shaded portion.
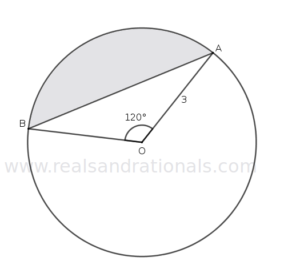
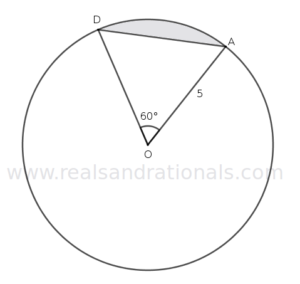
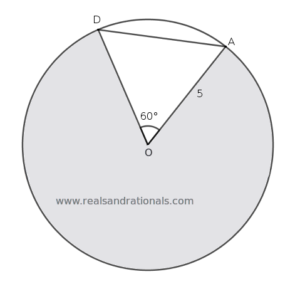
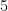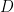  4. In the following figure, a circle with center O and radius 5 units is shown. A and D are two points on the circle such that \angle AOD = 60^\circ. And, a smaller circle is shown that has AD as its diameter.

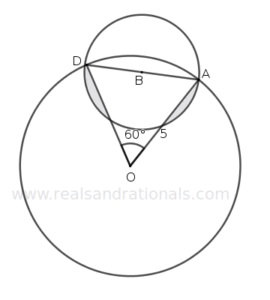
    1. What is the area of the small circle?
    2. What is the area of the shaded portion?