Naming
Exercises
Problem set
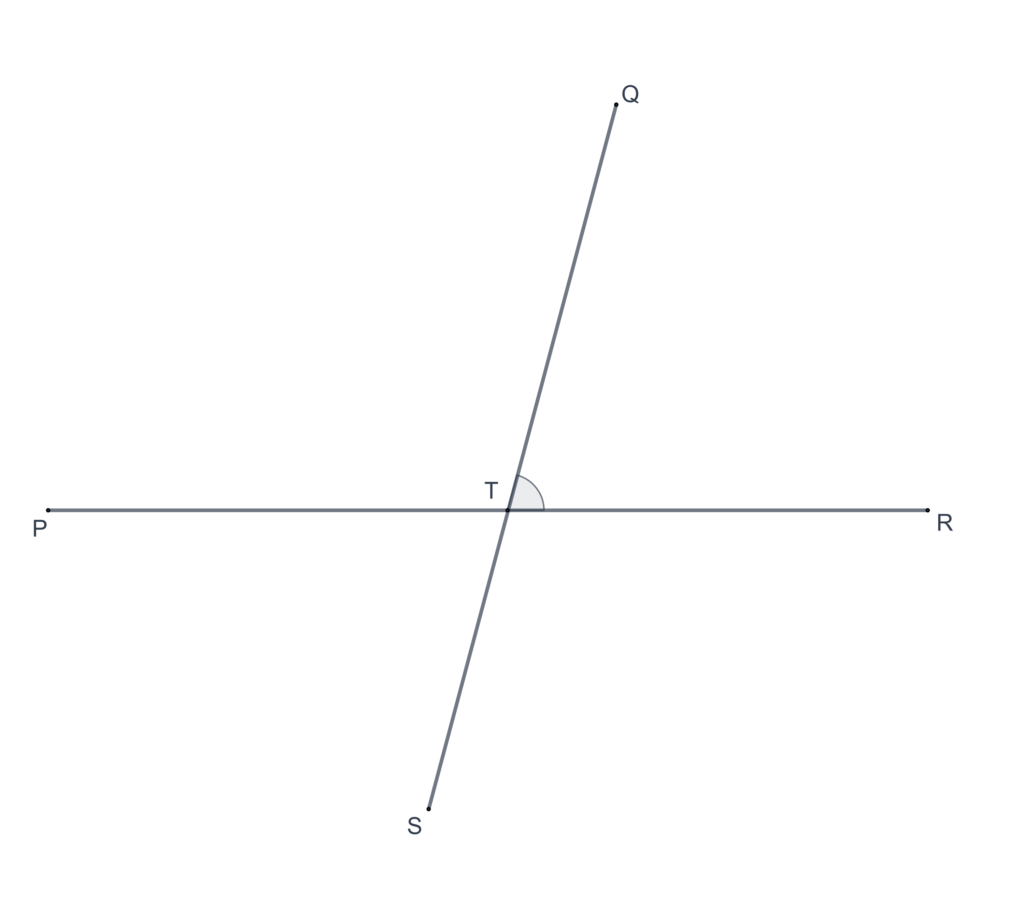
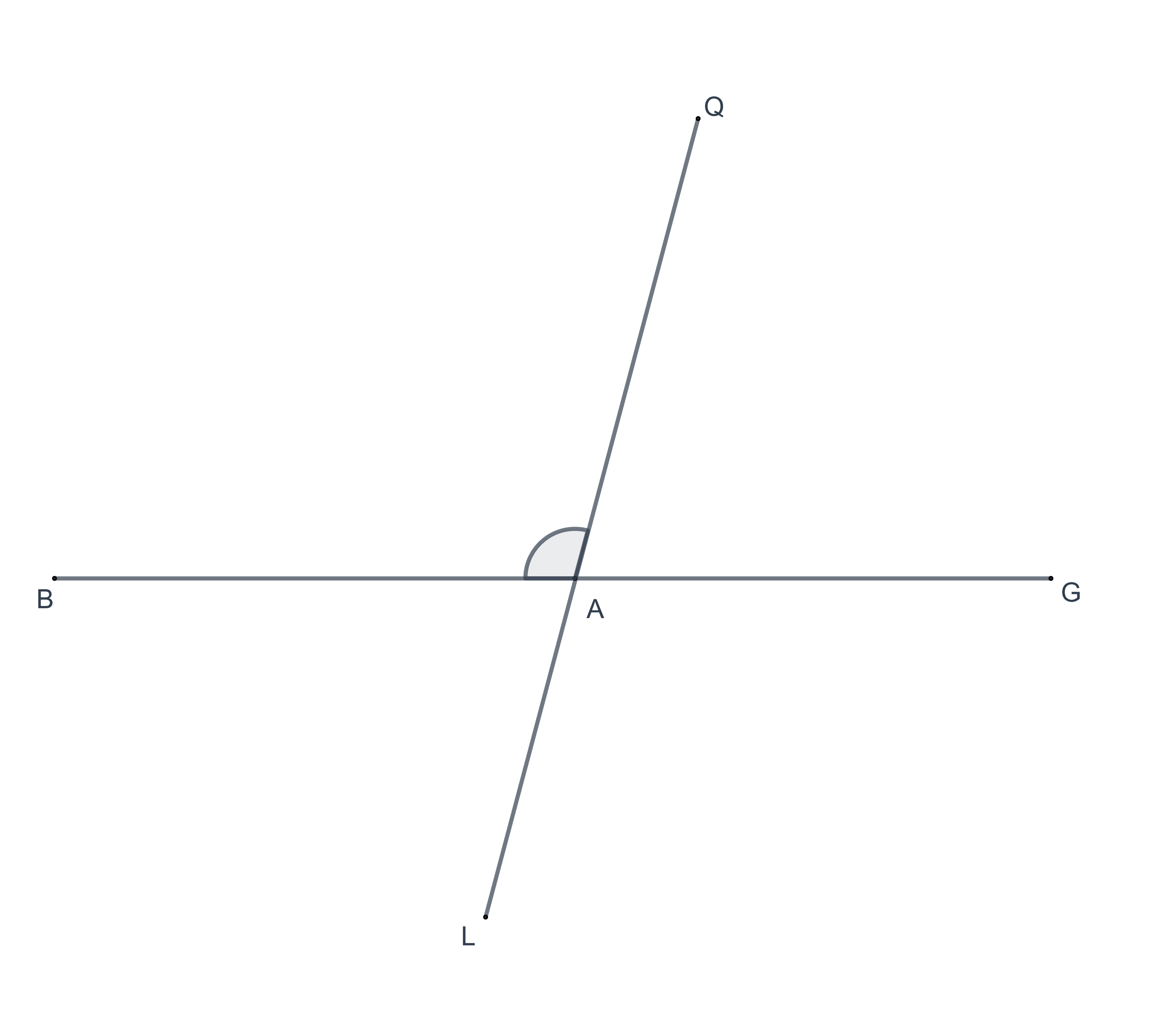
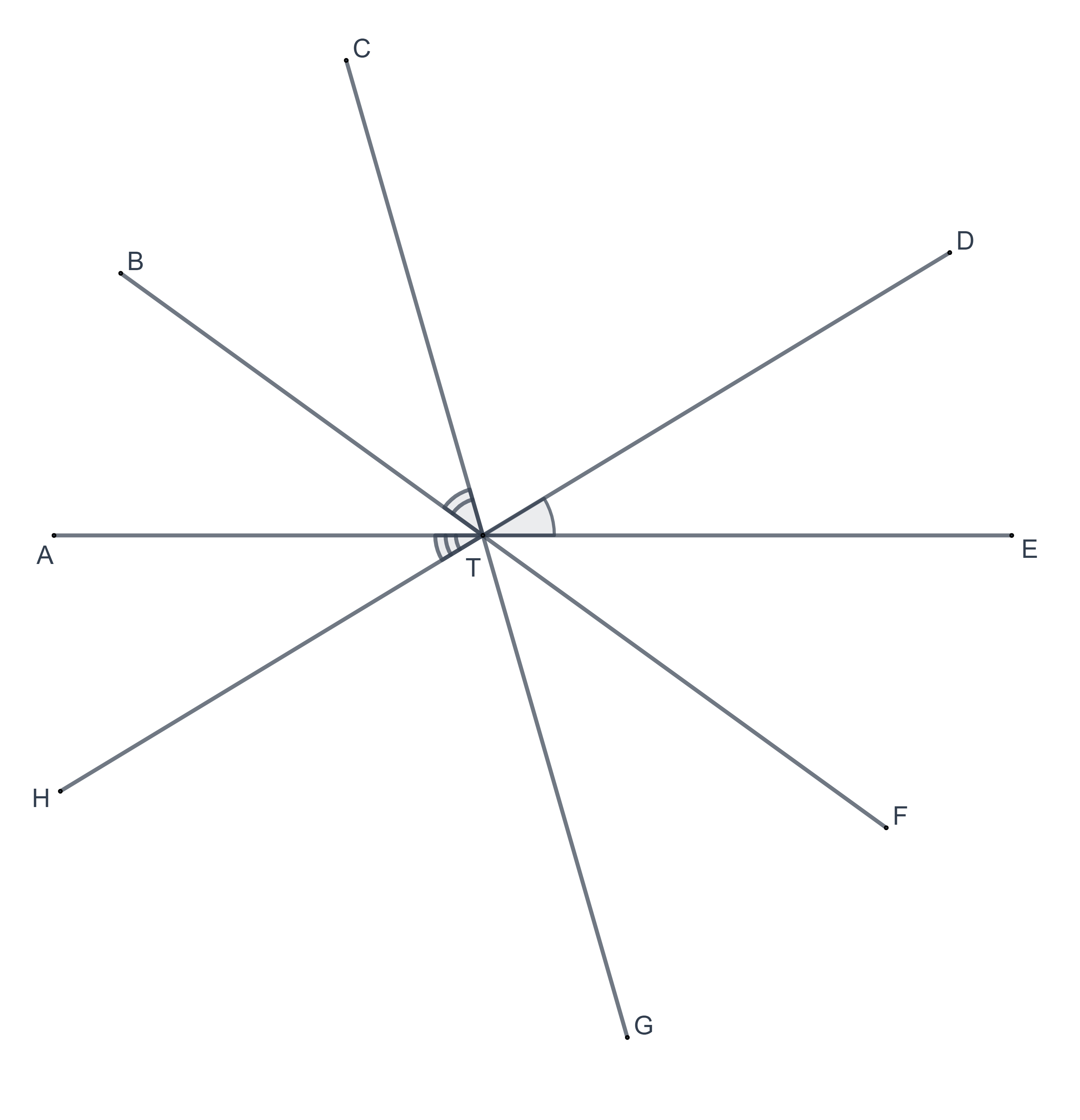
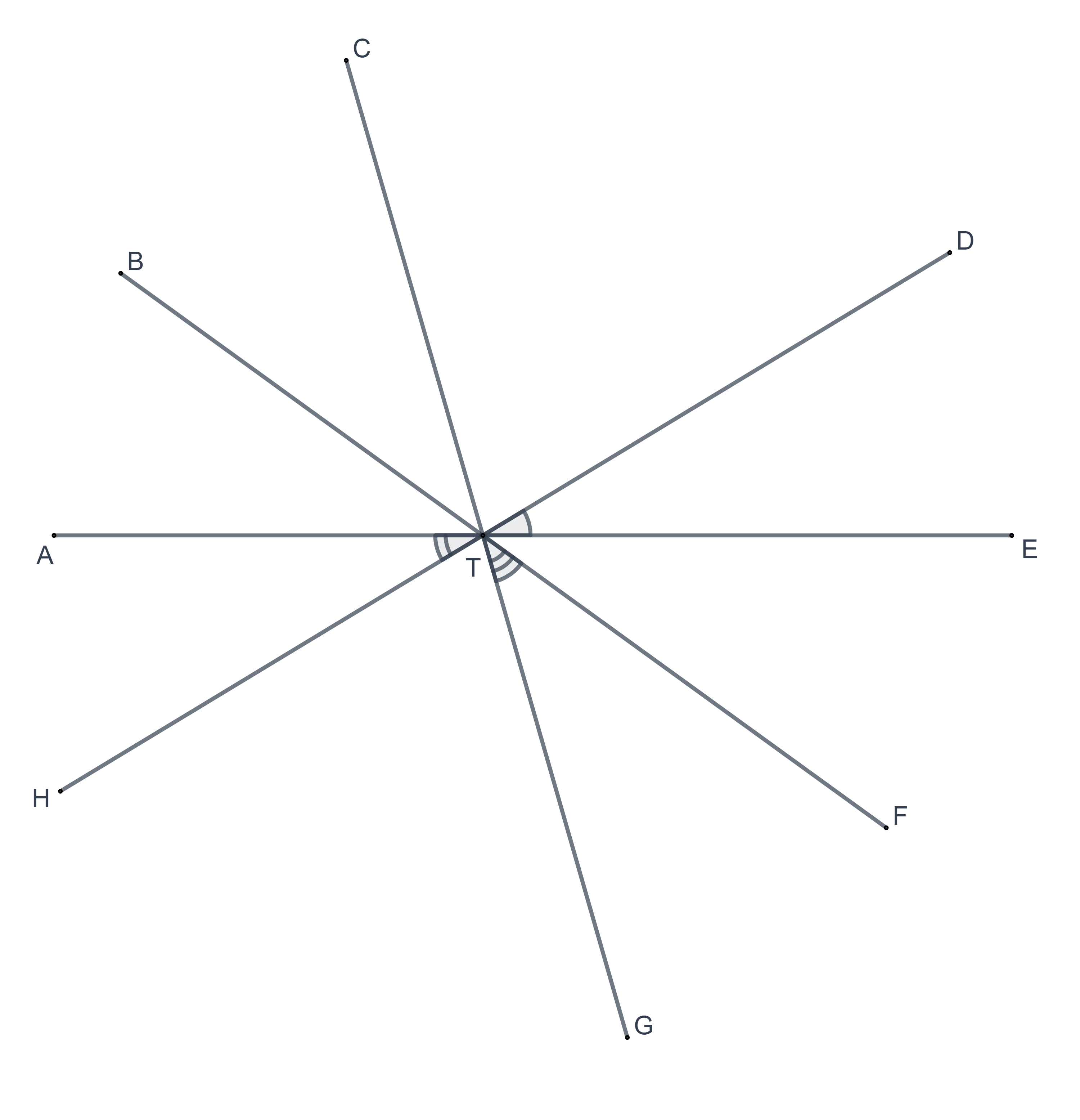
In each of the following figures, give the three-letter names for the marked angles.
Intersecting lines
Exercises
Problem set
- In the following figure, what is the measure of
?
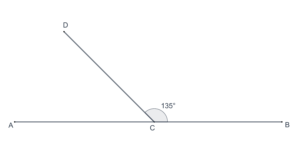
- In the following figure, what is the measure of
?
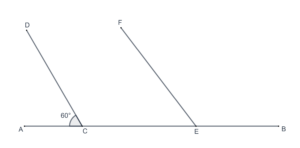
- In the following figure, what are the measures of
and
?
- In the following figure, what are the measures of
and
?
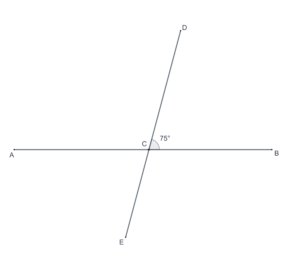
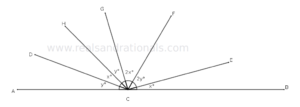
- In the following figure,
is a straight line segment. What is the measure of
?
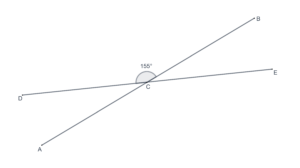
- In the following figure,
. What is the measure of
?
Parallel lines
Exercises
Problem set
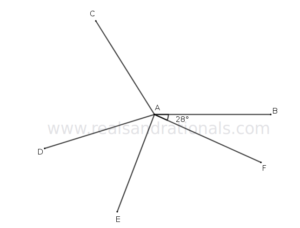
- In the following figure,
. What are the measures of
and
?
- In the following figure,
. What are the measures of
and
?
- In the following figure,
. What is the value of
?
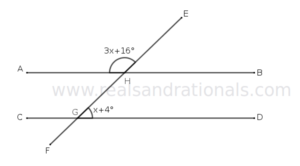
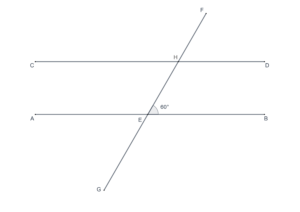
- In the following figure,
. What is the measure of
?
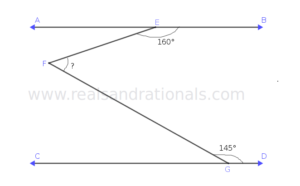
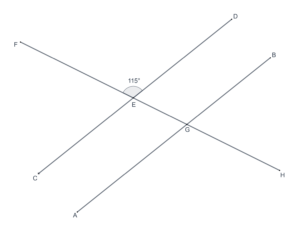
- In the following figure,
. What is the measure of
?
Problem set
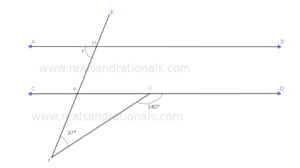
- In the following figure,
. What is the measure of
?
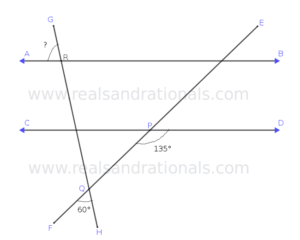
- In the following figure,
and
. What is the measure of
?
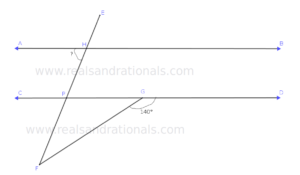
- In the following figure,
, and
. What is the measure of
?
Problem set
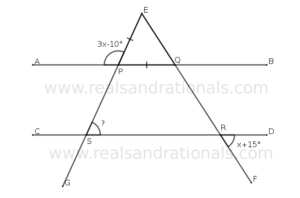
- In the following figure,
,
and
is a straight line segment. What is the measure of
?
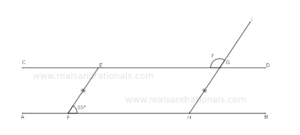
- In the following figure,
,
and
is a straight line segment. What is the measure of
?
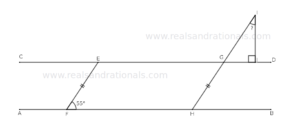
- In the following figure,
is a trapezoid with
. What is the measure of
?

- In the following figure,
,
. What is the measure of
?
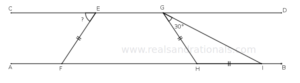
- In the following figure,
,
, and
and
are straight line segments. What is the measure of
?
Triangles
Exercises
Problem set
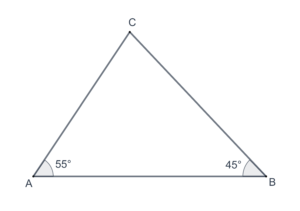
- In the following figure, what is the measure of
?
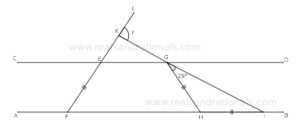
- In the following figure, what is the measure of
?
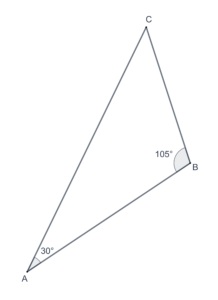
- In the following figure, what is the measure of
?
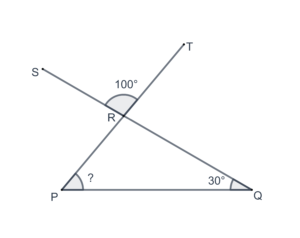
- In the following figure, what is the measure of
?
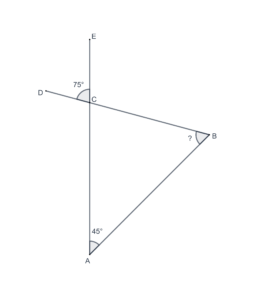
- In the following figure, what is the measure of
?
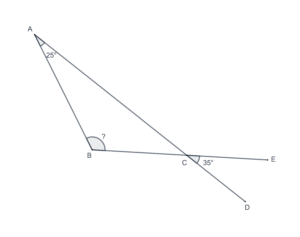
- In the following figure, what is the measure of
?
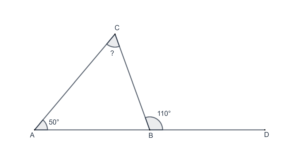
Problem set
- In the following figure, what is the measure of
?
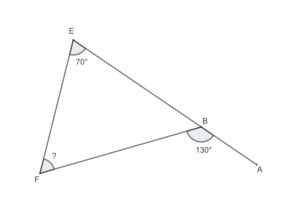
- In the following figure, what is the measure of
?
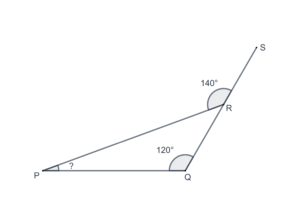
- In the following figure, what is the measure of
?
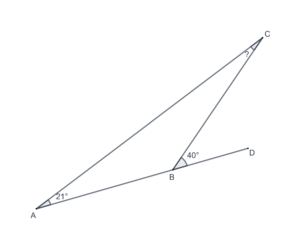
- In the following figure, what is the measure of
?
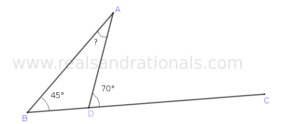
- In the following figure,
and
are three straight line segments. What is the measure of
?
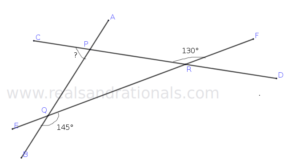
- In the following figure,
is a straight line segment. what is the measure of
?
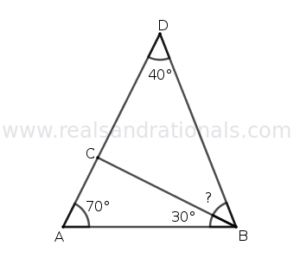
Problem set
- In the following figure,
and
is a straight line segment. What is the measure of
?
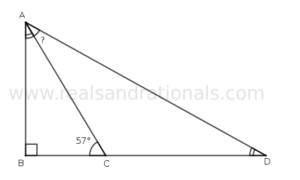
- In the following figure,
is a straight line segment. What is the value of
?
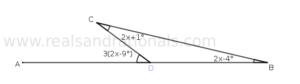
- In the following figure,
is a straight line segment. And,
and
. What is the measure of
?
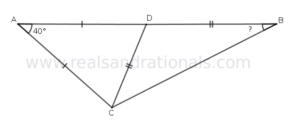
- In the following figure,
is a straight line segment. What is the measure of
?
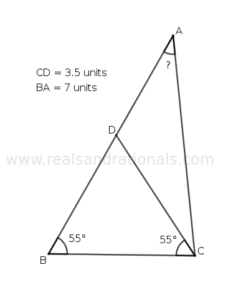
- In the following figure,
is a straight line segment. What is the length of segment
?
Problem set
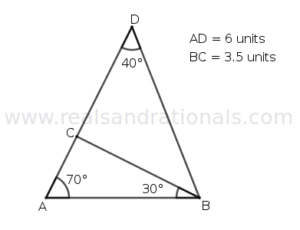
- In the following figure,
is a straight line segment. What is the measure of
?
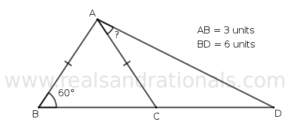
- In the following figure,
is a right triangle. And,
and
. What is the measure of
?
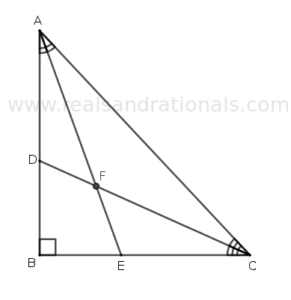
- In the above figure, if
, what is the measure of
?
Polygons
Exercises
Problem set
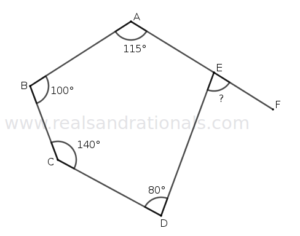
- In the following,
is a straight line segment. What is the measure of angle
?
- What is the measure of each of the interior angles of a regular pentagon?
- What is the measure of each of the interior angles of a regular hexagon?
- The measure of the interior angle of a regular polygon is
. How many sides does the polygon have?
- The measure of the interior angle of a regular polygon is
. How many sides does the polygon have?
Problem set
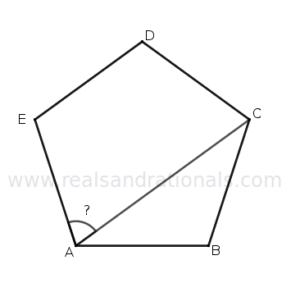
- In the following figure,
is a regular polygon. What is the measure of
?
- In an octagon, the interior angles are in the ratio
. What is the measure of the smallest angle?
- One angle of a hexagon is
. Remaining angles of the hexagon are in the ratio
. What is the biggest angle of the hexagon?
- Two of the interior angles of a hexagon are
and
. Of the remaining four angles, the measures of the first and the second are in the ratio
, the measures of the second and the third are also in the ratio
and the measures of the third and the fourth are also in the ratio
. What is the measure of the biggest angle?
Radian measure
Definition of 1 radian
Exercises
Problem set
- An arc on the circumference of a circle subtends (makes) an angle of
at the center of the circle, and the length of the arc is
units. Another arc on the circumference of the same circle subtends an angle of
. What is the length of the second arc?
- An arc on the circumference of a circle subtends (makes) an angle of
at the center of the circle, and the length of the arc is
units. Another arc on the circumference of the same circle subtends an angle of
. What is the length of the second arc?
- An arc on the circumference of a circle subtends (makes) an angle of
at the center of the circle, and the length of the arc is
units. Another arc on the circumference of the same circle subtends an angle of
. What is the length of the second arc?
- An arc on the circumference of a circle subtends (makes) an angle of
at the center of the circle, and the length of the arc is
units. How much of an angle does a second arc of length
units on the circumference of the same circle subtend at the center of the circle?
- An arc on the circumference of a circle subtends (makes) an angle of
at the center of the circle, and the length of the arc is
units. How much of an angle does a second another arc of length
units on the circumference of the same circle subtend at the center of the circle?
Problem set
- A circle has radius
units. An arc on the circumference of the circle subtends(makes) an angle of
radian at the center of the circle. What is the length of the arc?
- A circle has radius
cm. What is the measure of the angle in radians that is subtended (made) by an arc of length
cm at the center of the circle?
- A circle has radius
units. An arc on the circumference of the circle subtends(makes) an angle of
radians at the center of the circle. What is the length of the arc?
- A circle has radius
units. An arc on the circumference of the circle subtends(makes) an angle of
radians at the center of the circle. What is the length of the arc?
- A circle has radius
cm. What is the measure of the angle in radians that is subtended (made) by an arc of length
cm at the center of the circle?
- A circle has radius
cm. What is the measure of the angle in radians that is subtended (made) by an arc of length
cm at the center of the circle?
- A circle has radius
m. What is the measure of the angle in radians that is subtended (made) by an arc of length
m at the center of the circle?
- A circle has radius
m. What is the measure of the angle in radians that is subtended (made) by an arc of length
m at the center of the circle?
- A circle has radius
cm. What is the length of the arc that subtends (makes) an angle of
radians at the center?
- In a circle, an arc of length
cm subtends (makes) an angle of
radians at the center of the circle. What is the radius of the circle?
Conversion from degrees to radians
Exercises
Problem set
Express each of the following in radian measure.
Problem set
Express each of the following in radian measure.
Problem set
Express each of the following in radian measure.
Problem set
Express each of the following angles as , where
. For example,
. Then, use such expressions to convert each of the given angles into radian measure.
Problem set
Express each of the following in radian measure.
Problem set
Express each of the following angles as , where
. For example,
. Then, use such expressions to convert each of the given angles into radian measure.
Problem set
Express each of the following angles as , where M is either a multiple of
and
. For example,
. Then, use such expressions to convert each of the given angles into radian measure.
Conversion from radians to degrees
Exercises
Problem set
Express each of the following in degrees.
Problem set
Express each of the following in degrees.
Problem set
Express each of the following angles as , where M is a multiple of
and
. For example,
. Then, use such expressions to convert each of the given angles into degrees.
Application of concept
Exercises
Problem set
- A circle has radius
units. An arc on the circumference of the circle subtends (makes) an angle of
at the center of the circle. What is the length of the arc?
- A circle has radius
units. An arc on the circumference of the circle subtends (makes) an angle of
at the center of the circle. What is the length of the arc?
- A circle has radius
units. An arc on the circumference of the circle subtends (makes) an angle of
at the center of the circle. What is the length of the arc?
- Two circles are drawn. First circle has radius
units, and the second circle has radius
units. An arc of length
units on the circumference of the first circle subtends (makes) an angle of
at the center of the circle. What is the length of the arc on the circumference of the second circle that subtends an angle of
at the center of the second circle?
- Two circles have radii in the ratio
. An arc of length
cm in the smaller circle subtends (makes) an angle of
at the center. What would be the length of the arc in the bigger circle that subtends the same angle?
- Two circles have radii in the ratio
. An arc in the bigger circle has has length that is
times the length of an arc in the smaller circle. What is the ratio of angles subtended (made) by the two arcs at the respective centers?
- Two circles have radii in the ratio
. An arc in the bigger circle has has length that is
times the length of an arc in the smaller circle. What is the ratio of angles subtended (made) by the two arcs at the respective centers?
Problem set
- In an isosceles triangle, each of the equal angles is
radians. What is the measure of the third angle in radians?
- Two radii are drawn for a circle to have an arc of length
feet between them. The angle subtended by the two radii is
. What is the radius of the circle?
is a regular octagon. What is the angular measure of each of its interior angles in radians?