- 1 Similar triangles
- 2 Special triangles
- 3 Definitions of ratios in right triangle context
- 4 Ratios of complimentary angles
- 5 Definitions of ratios in unit circle context
- 6 Miscellaneous
Similar triangles
Exercises
Problem set
-
In each of the following problems,
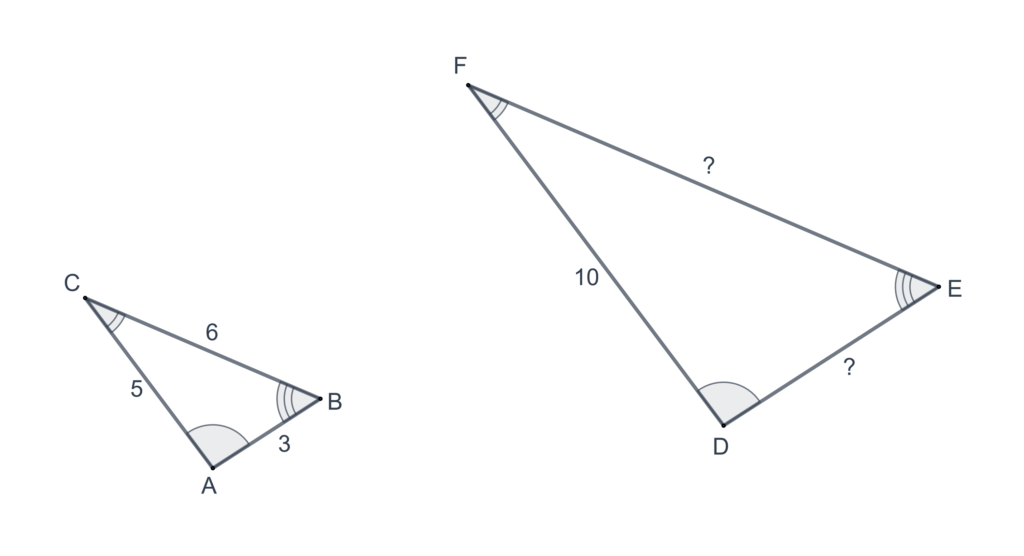
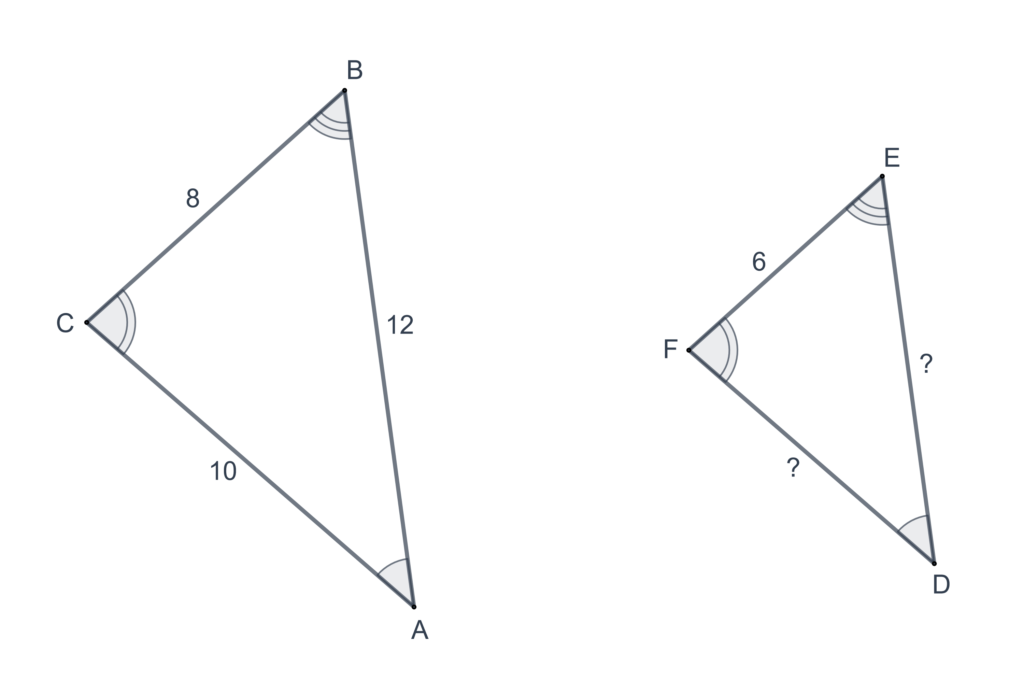
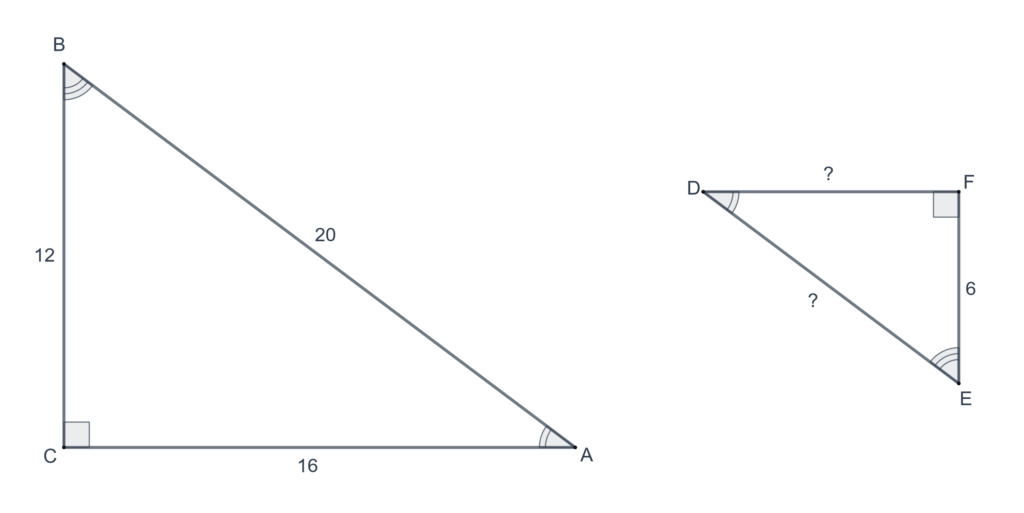
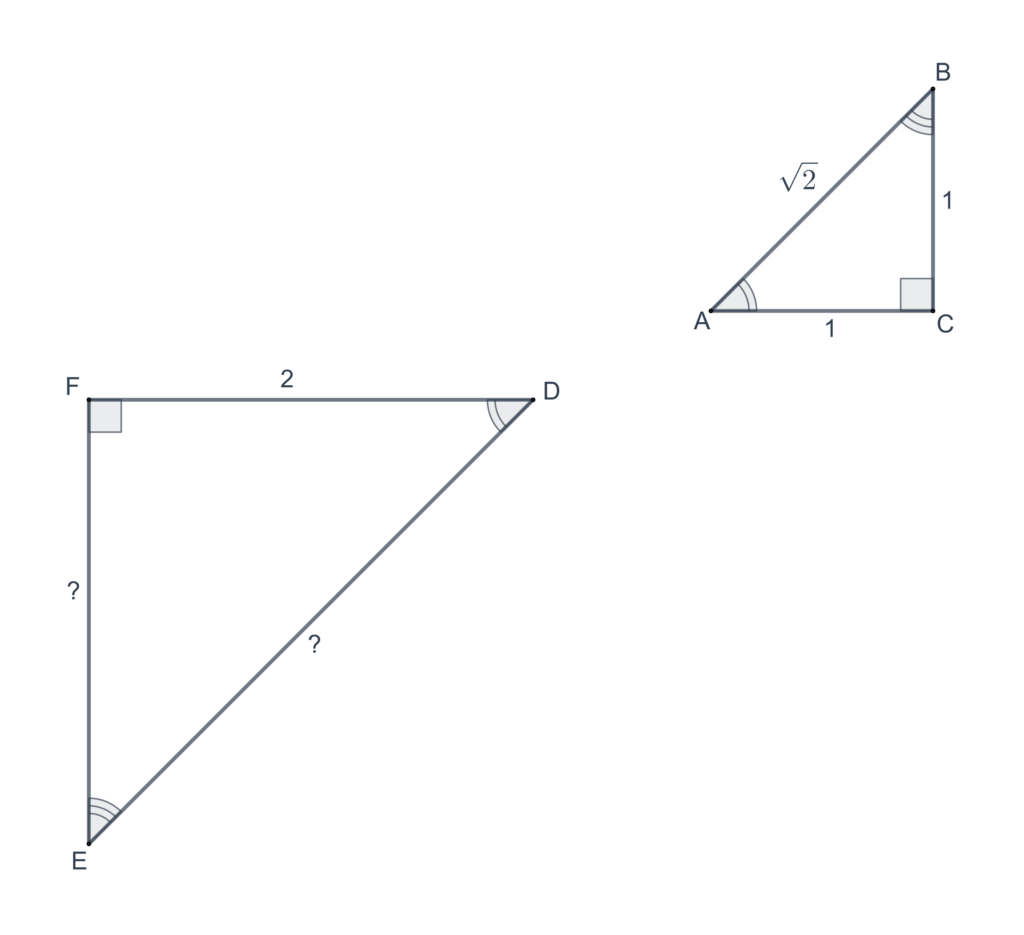
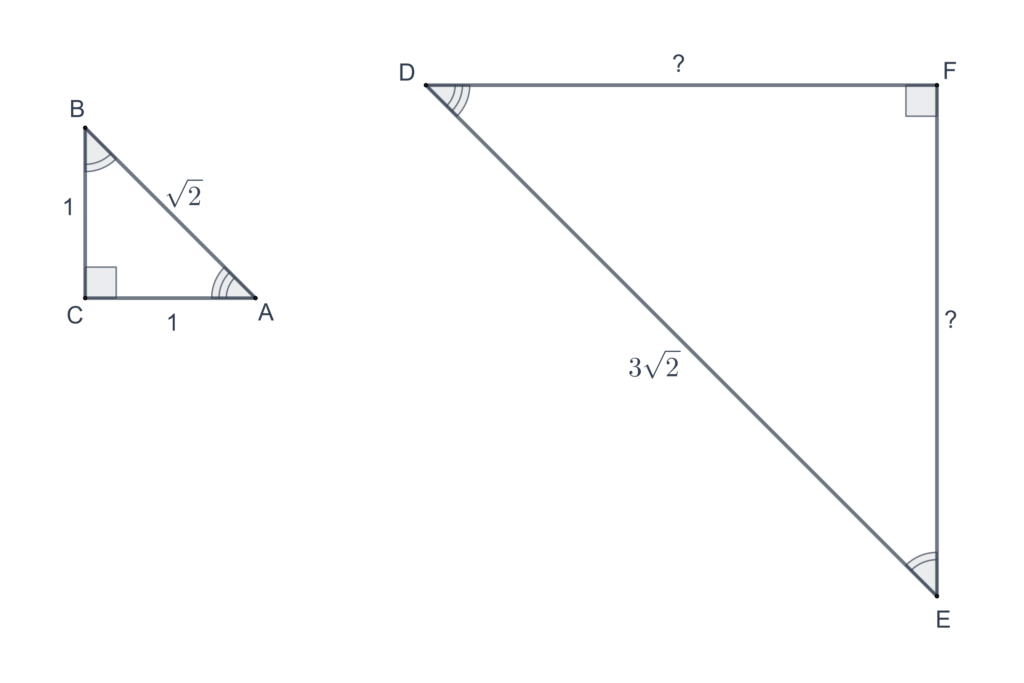
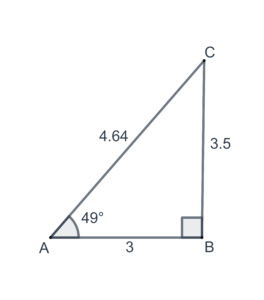
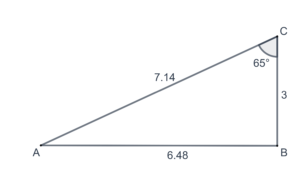
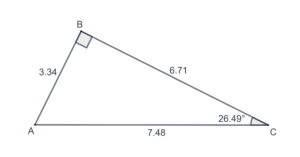
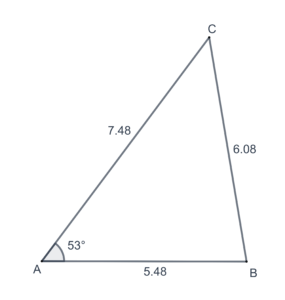
- Find
, if
.
- Find
, if
.
- Find
, if
.
- Find
, if
.
- Find
, if
.
- Find
, if
.
- Find
, if
.
- Find
, if
.
- Find
, if
.
- Find
, if
.
- Find
, if
.
- Find
, if
.
- Find
, if
.
- Find
, if
.
- Find
, if
.
- Find
, if
.
- Find
, if
.
. Find
.
. Find
.
. Find
.
. Find
.
. Find
.
. Find
.
. Find
.
. Find
.
. Find
.
. Find
.
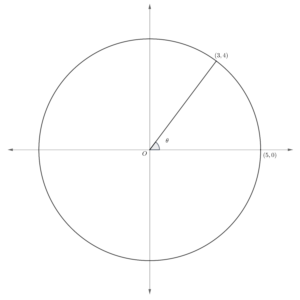
- In the following diagram, a circle is drawn with its center at the origin of a coordinate plane, and a radius making angle
with X-axis is shown. Find the values of
,
and
.
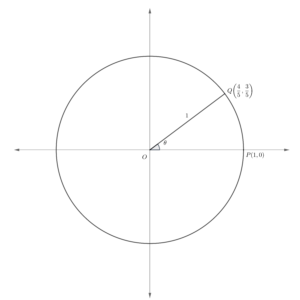
- In the following diagram, a circle is drawn with its center at the origin of a coordinate plane, and a radius making angle
with X-axis is shown. Find the values of
,
and
.
- Express
in terms of
and
.
- Express
in terms of
and
.
- Express
in terms of
and
.
- Express
in terms of
and
.
- Express
in terms of
and
.
- Express
in terms of
and
.
- Express
in terms of
and
.
- Which of the following is
equal to:
or
?
- Which of the following is
equal to:
or
?
- Using right triangle
, express
in terms of
and
. Hint: Use problem 2.
- Which of the following is
equal to:
or
?
- Express
in terms of
.
- Express
in terms of
.
- Using right triangle
, express
in terms of
and
. Hint: Use problems 4 and 6.
- Express
in terms of
and
. Hint: Use problems 1, 3 and 7.
- For
, what are the minimum and maximum values of
,
and
?
- For
, what are the minimum and maximum values of
,
and
?
- For
, find the minimum and maximum values of
and
.
- For
, find the minimum and maximum values of
.
- For
, find the minimum and maximum values of
.
- For
, find the minimum and maximum values of
.
- For
, find the minimum and maximum values of
.
- For
, find the minimum and maximum values of
.
- For
, find the minimum and maximum values of
.
- For
, find the minimum and maximum values of
.
- For
, find the minimum and maximum values of
.
- For
, find the minimum and maximum values of
.
- For
, find the minimum and maximum values of
.
- For
, find the minimum and maximum values of
.
- Say,
. Explain the minimum and maximum possible values of
and
?
- Prove:
- Prove:
Special triangles
Exercises
Problem set
For the following problems, assume is a right triangle with
. For each problem, given the measures of one angle and one side, find the measures of the other two sides of the triangle. Do not use trigonometric ratios to solve these.
Problem set
For the following problems, assume is a right triangle with
. For each problem, given the measures of one angle and one side, find the measures of the other two sides of the triangle. Do not use trigonometric ratios to solve these.
Problem set
For the following problems, assume is a right triangle with
. For each problem, given the measures of one angle and one side, find the measures of the other two sides of the triangle. Do not use trigonometric ratios to solve these.
Definitions of ratios in right triangle context
Exercises
Problem set
In each of the following problems, find using the figure given.
Problem set
Find the values of the following using a geometry toolbox or geometry software. Do not use a calculator.
Problem set
In each of the following problems, assume we have a right triangle with
and
.
Problem set
In each of the following problems, assume we have a right triangle with
and
.
Problem set
In each of the following problems, assume we have a right triangle with
and
.
Problem set
For the following problems, assume is a right triangle with
. For each problem, given the measures of one angle and one side, find the measures of the other two sides of the triangle.
Ratios of complimentary angles
Exercises
Problem set
In each of the following problems, is one of the acute angles in a right triangle.
Problem set
In each of the following problems, is one of the acute angles in a right triangle.
Definitions of ratios in unit circle context
Exercises
Motivation
Problem set
Angles between 0 degrees and 360 degrees
Problem set
Find the values of the following.
Problem set
Find the values of the following.
Problem set
Find the values of the following.
Problem set
Find the values of the following.
Problem set
Evaluate the following
Angles greater than 360 degrees
Problem set
Evaluate the following.
Problem set
Evaluate the following.
Problem set
Express each of the following angles as , where M is a multiple of
and
. For example,
. Then, show a line segment making the specified angle with positive
-axis of a coordinate plane.
Problem set
Express each of the following angles as , where M is a multiple of
and
. For example,
. Then, show a line segment making the specified angle with positive
-axis of a coordinate plane.
Problem set
Express each of the following angles as , where M is a multiple of
and
. For example,
. Then, show a line segment making the specified angle with positive
-axis of a coordinate plane.
Problem set
Express each of the following angles as , where M is a multiple of
and
. For example,
. Then, show a line segment making the specified angle with positive
-axis of a coordinate plane.
Problem set
Evaluate the following
Problem set
Evaluate the following
Problem set
Evaluate the following
Problem set
Evaluate the following
Problem set
Evaluate the following
Negative angles
Problem set
Evaluate the following
Problem set
Evaluate the following
Problem set
Evaluate the following
Problem set
Express each of the following angles as , where M is a multiple of
and
. For example,
. Then, show a line segment making the specified angle with positive
-axis of a coordinate plane.
Problem set
Express each of the following angles as , where M is a multiple of
and
. For example,
. Then, show a line segment making the specified angle with positive
-axis of a coordinate plane.
Problem set
Express each of the following angles as , where M is a multiple of
and
. For example,
. Then, show a line segment making the specified angle with positive
-axis of a coordinate plane.
Problem set
Evaluate the following
Problem set
Evaluate the following
Problem set
Evaluate the following
Miscellaneous
Exercises
Problem set
In each of the following problems, determine the value of , if
is one of the acute angles in a right triangle.
Problem set
For the following problems, assume .
Problem set
Find the reference angle of each of the following.
Problem set
For each of the following, find the reference angle for the angle involved. Then, use the reference angle and the ASTC mnemonic to evaluate the trigonometric ratio.
Problem set
Find the reference angle of each of the following.
Problem set
In the following, assume . There are two blanks to be filled on the right hand side of each of the problems. Fill in the blanks appropriately. Use
or
for the first blank, and one of the six trigonometric ratios (
) for the second blank. For example, if
, the first blank takes
and the second blank takes
.
Problem set
In the following figure, and
. Line segments
and
are constructed such that
and
are all right angles. And,
unit.
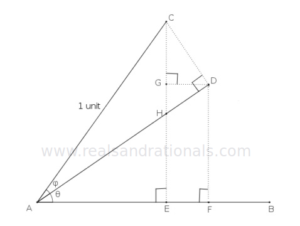
The following problems are based on the above figure.