Learn – Algebra foundations – Functions

Definition and notation

Exercises

Problem set

  1. Say, you are doing a summer job. Your goal is to earn a certain money so that you could buy a computer for yourself. You are wondering how you might earn that much money. What is a good independent quantity that the money you earn over summer would depend on?
  2. A pediatrician is trying to model the height of kid as a mathematical function. What is a good independent quantity that the height of the kid could be related to? (Think of what physical quantity that the height of the kid would depend on.)
  3. A family is planning a vacation to Orlando, and is estimating how much it costs them for hotel stay on the trip. They would like to model the total hotel cost using a mathematical function. What is a good independent quantity that the cost could be related to?
  4. A paving company is estimating the time it would take to pave a street. They would like to model the time taken as a mathematical function. What is a good independent quantity that time taken could be related to? (Think of what physical quantity that time taken would depend on.)
  5. A city council is making some plans for the city development based on how the population of the city grew in the past. They would like to model the population using a mathematical function. What is a good independent quantity that population could be related to?

Problem set

  1. The cost of a pound of tomatoes at a grocery store is \$2.
    1. Using some example values for pounds of tomatoes, give a function table to show how cost changes depending on the pounds of tomatoes.
    2. Assuming the function is called f, give the values of f(3) and f(7). Note that the function takes number of pounds of tomatoes as input and gives cost as output.
  2. A car requires 1 gallon of gas to drive 15 miles.
    1. Using some example values for number of miles, give a function table to show how the amount of gas required depends on the number of miles to be driven.
    2. Assuming the function is called f, give the values of f(75) and f(150). Note that the function takes number of miles as input and gives amount of gas required as output.
  3. Marvin takes 30 mins to mow 10000 square feet of yard. If a function f takes amount of square feet of yard as input and gives the time Marvin takes to mow as output, give the values of the following:
    1. f(20000)
    2. f(5000)
    3. f(90000)
  4. A salesman is selling dishwashers at a price of \$300 a piece. The salesman earns a profit of 10\% on each sale. If a function f takes number of dishwashers sold as input and gives the profit earned as output, give the values of the following:
    1. f(2)
    2. f(10)
    3. f(50)

Representing using expressions

Exercises

Problem set

In each of the following problems, form a function table for the function specified. Assuming the name of the function is f and the independent variable is x, give an expression for f(x).

  1. At a grocery store, the cost of bananas is \$0.69 per pound. The function takes number of pounds of bananas as input, and gives the cost as output.
  2. At Mama’s Groceries, the cost of mangoes is \$2.50 per pound. The store also charges a bagging fee of 5c per pound. The function takes number of pounds of mangoes as input, and gives the total cost (including the bagging fee) as output.
  3. At a day care center, cost for registering a baby is \$50.00, while the recurring monthly cost is \$675.00. The function takes number of months that the baby has been going to the day care as input, and gives the total cost incurred for the baby as output.
  4. I was looking to buy notebooks from an online bookstore. The cost of each notebook is \$3.75. The store charges \$7.00 for shipping and handling. The function takes number of notebooks as input, and gives the total cost (including shipping and handling) as output.
  5. Currently, Jane has \$35000.00 in her bank. She plans on saving \$ 12000.00 every year, and depositing that into her bank account. The function takes number of years from now as input, and gives the total money in dollars that Jane expects to have in her bank account as output.
  6. Jane’s car gives 19 miles for every gallon of gasoline. The function takes number of miles driven as input and gives the number of gallons consumed as output.

Problem set

  1. Nathan was shopping for balloons at an online store. The store sells the balloons in sets of 12. Cost of each set is \$2.50. The store charges a sales tax of 6\% of the cost of items bought, and \$3.99 for shipping and handling. Express the total amount Nathan would have to pay as a function of number of sets of balloons. Identify the domain of the function.
  2. Ryan and Rita are looking to buy a house. They find that the house prices in their locality start at a base price of \$300,000 and go all the way to \$500,000.Assume there is a realtor fee of 3\% (of the house price) and a county registration fee of \$1000 that Ryan and Rita need to pay when buying a house. Express the total amount they need to pay as a function of the house price. Identify the domain of the function.
  3. On a summer day, the temperature in Washington DC was measured to be 70^\circ\mbox{F}. It was also observed that going north from Washington DC, the temperature drops by 1.5^\circ\mbox{F} for every 50 miles. Give an expression for temperature at a northern location as a function of its distance from Washington DC. Identify the domain of the function.
  4. Betsy is able to paint 35 square feet in three hours. Express the time it takes for her to paint as a function of area in square feet. Identify the domain of the function.
  5. Don mows 100 square feet of his yard in 30 minutes. But, after 30 minutes, his pace decreases to 50 square feet every 30 minutes. Assuming he mows for more than 30 minutes, express the area he mows as a function of time. Identify the domain of the function.
  6. Ralph works a minimum of 8 hours a working day. And, he earns \$200.00/day on a regular 8-hour working day. Occasionally, when work demands him to stay longer at work, he gets paid at \$1.00 for every minute that he works beyond the 8-hour requirement. Express the dollar amount that he makes in a day as a function of the total time he spends at work on a given working day.

Problem set

  1. Current population of bacteria in a laboratory dish is approximately 320,000. Every minute the population of the bacteria doubles. Express what the population of bacteria would be as a function of number of minutes from now.
  2. Javier is estimating his daily heating expenses during a winter. His heating doesn’t turn on on any day if the outside temperature is equal to or above 55^\circ\mbox{F}, but he incurs cost if the temperature drops below 55^\circ\mbox{F}. His estimated heating cost is as follows:

    \begin{aligned} &55^\circ\mbox{F or above} &:&\mbox{ }\$0.00 \\ &54^\circ\mbox{F} &:&\mbox{ }\$1.00 \\ &53^\circ\mbox{F} &:&\mbox{ }\$2.00 \\ &52^\circ\mbox{F} &:&\mbox{ }\$4.00 \\ &51^\circ\mbox{F} &:&\mbox{ }\$8.00 \\ &50^\circ\mbox{F} &:&\mbox{ }\$16.00 \end{aligned}

    Essentially, the heating cost doubles for every degree drop in temperature. Express the estimated heating cost as a function of the outside temperature.

Problem set

  1. If f(x) = 5x-3, what does the function f output for each of the following input values?
    • 10
    • -2
  2. If h(x) = -4x+7, what does the function h output for each of the following input values?
    • -2
    • 2
  3. If g(x) = -x, what does the function g output for each of the following input values?
    • -10
    • 10
    • 0
  4. If g(x) = -7x-10, what does the function g output for each of the following input values?
    • -2
    • 3
    • 0
  5. If h(x) = x^2+3, what does the function h output for each of the following input values?
    • -3
    • 3
  6. If l(x) = 5-x^2, what does the function l output for each of the following input values?
    • 4
    • -4
  7. If f(x) = \sqrt{x-1}, what does the function output for each of the following input values?
    • 17
    • 4
    • 1
  8. If h(x) = |x|, what does the function output for each of the following input values?
    • -12
    • 123
    • 349.23
    • 0
  9. If t(x) = 0, what does the function output for each of the following input values?
    • \pi
    • 9.080088000888\cdots

Representing using graphs

Exercises

Problem set

For each of the following functions, give what the function outputs for each of the input values: -2, 0, 1. Assuming the name of the function is f, give the answer in function notation.








Not every relation is a function

Exercises

Problem set

  1. Is the relation between two quantities shown in the following table a function?

    \begin{array}{ |c|c| } \hline x & y \\ \hline 1 & 4 \\ 2 & 11 \\ 3 & 7 \\ 4 & 2 \\ 5 & 5 \\ \hline \end{array}

  2. Is the relation between two quantities shown in the following table a function?

    \begin{array}{ |c|c| } \hline x & y \\ \hline 1 & 1 \\ 4 & 2 \\ 9 & 3 \\ 16 & 4 \\ 25 & 5 \\ 1 & -1 \\ 4 & -2 \\ 9 & -3 \\ 16 & -4 \\ 25 & -5 \\ \hline \end{array}

  3. Is the relation between two quantities shown in the following table a function?

    \begin{array}{ |c|c| } \hline x & y \\ \hline 1 & 7 \\ 4 & 5 \\ 2 & 11 \\ 6 & 9 \\ 5 & 11 \\ 3 & 7 \\ \hline \end{array}

  4. Is the relation between two quantities shown in the following table a function?

    \begin{array}{ |c|c| } \hline x & y \\ \hline 6 & 7 \\ -4 & 5 \\ 2 & 11 \\ 6 & 9 \\ 5 & 11 \\ -3 & 7 \\ \hline \end{array}

  5. The human resources department at a company wants to represent the salary given to its employees as a mathematical relation. Is the relation a function?
  6. Is the relation between two kinds of quantities shown by the set of pairings \{(0,0),(1,1),(2,2),(3,3),(4,4),(-1,1),(-2,2),(-3,3),(-4,4)\} a function?

Problem set

Which of the following relations are functions? Assume the relations are from the set \mathbb{R} to the set \mathbb{R}. In case they are not functions, would restricting the sets in some way make them functions?

  1. \rho(x) = 1
  2. \gamma(x) = \frac{1}{x}
  3. \eta(x) = |x|
  4. \zeta(x) = \sqrt{x}
  5. \psi(x) = \sqrt[3]{x}
  6. x = (\kappa(x))^2
  7. x = 1

Domain and range

From representations as graphs

Exercises

Problem set

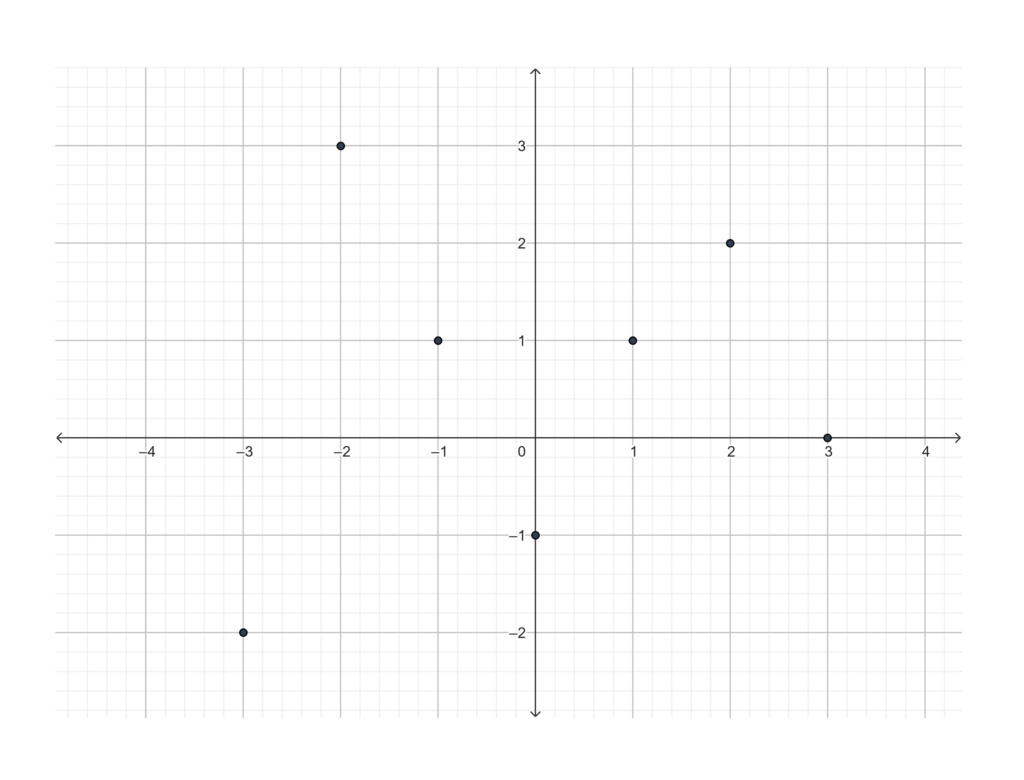
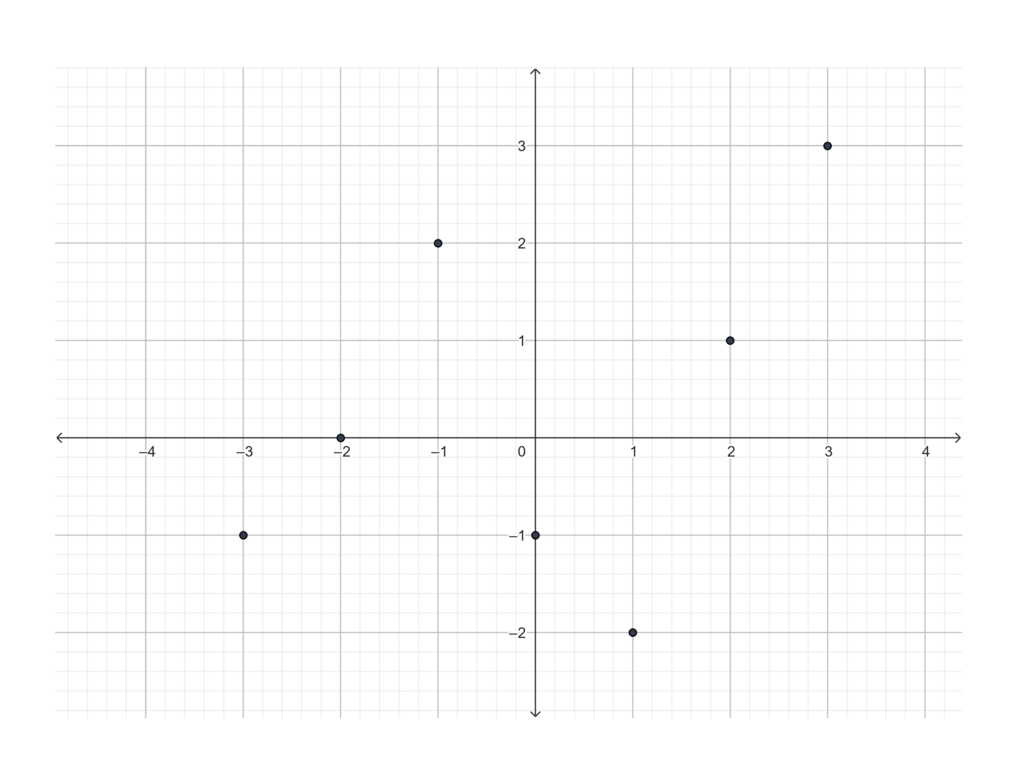
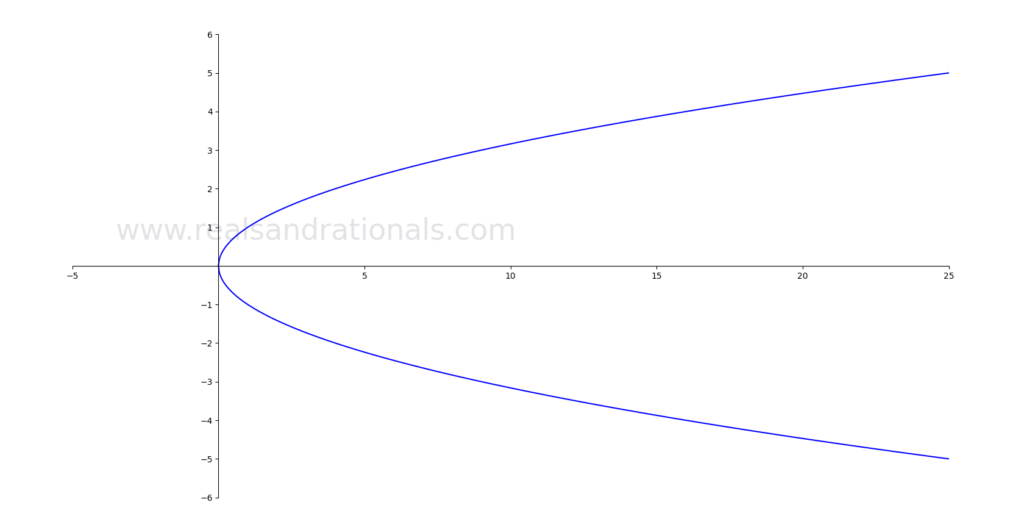
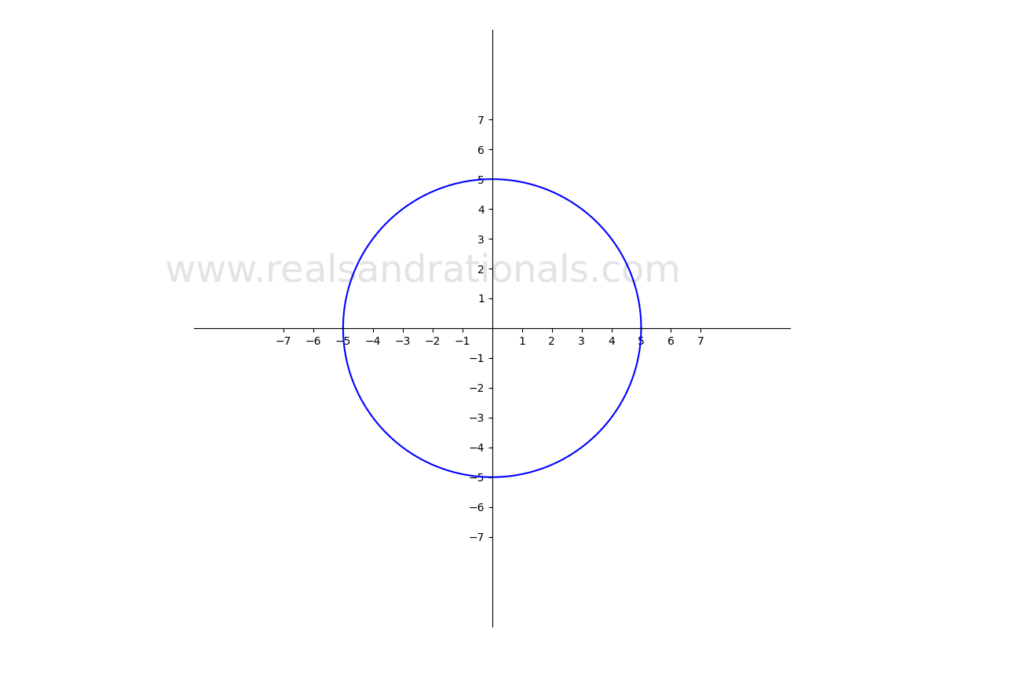
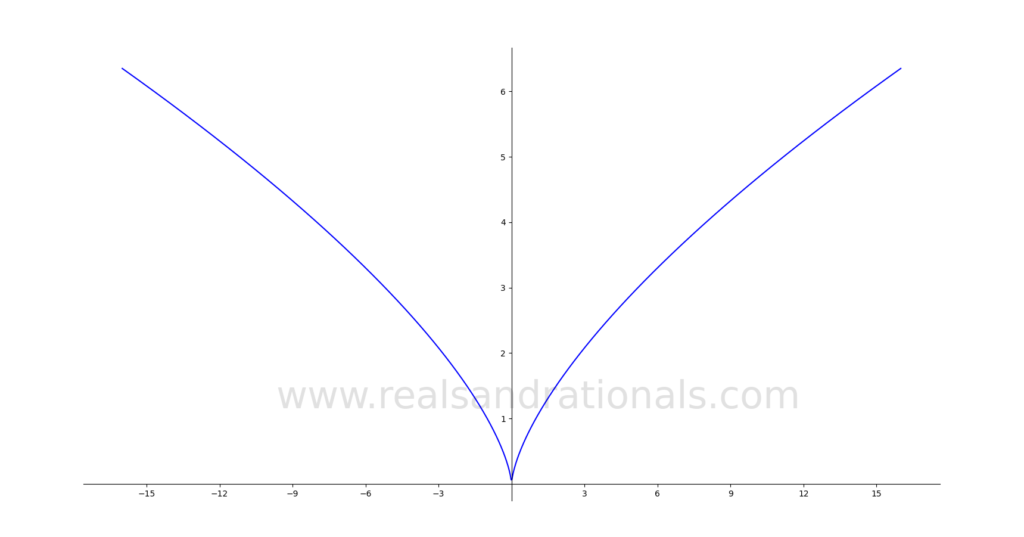
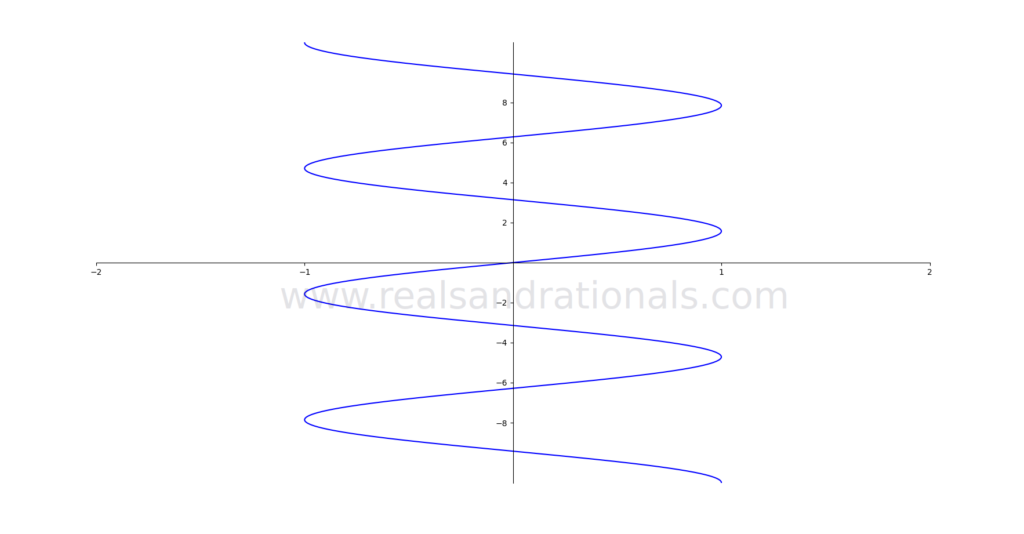
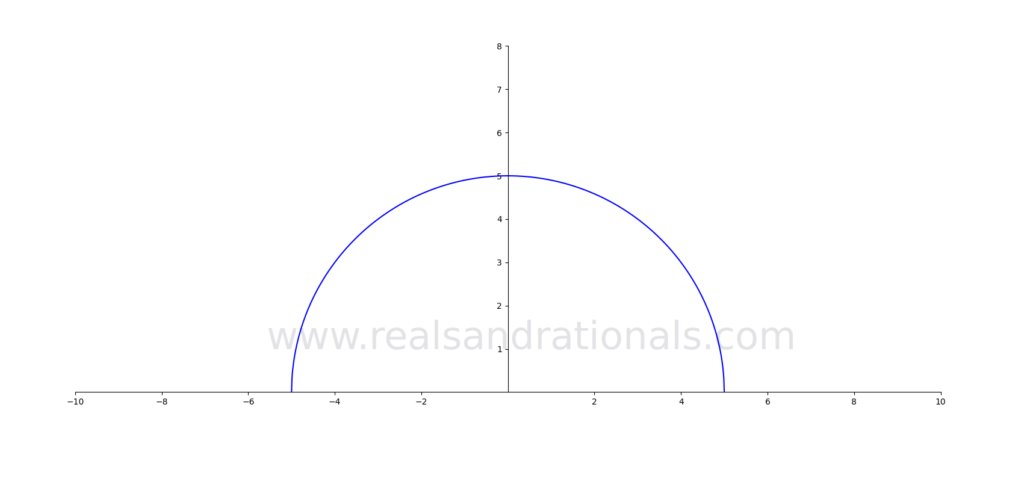
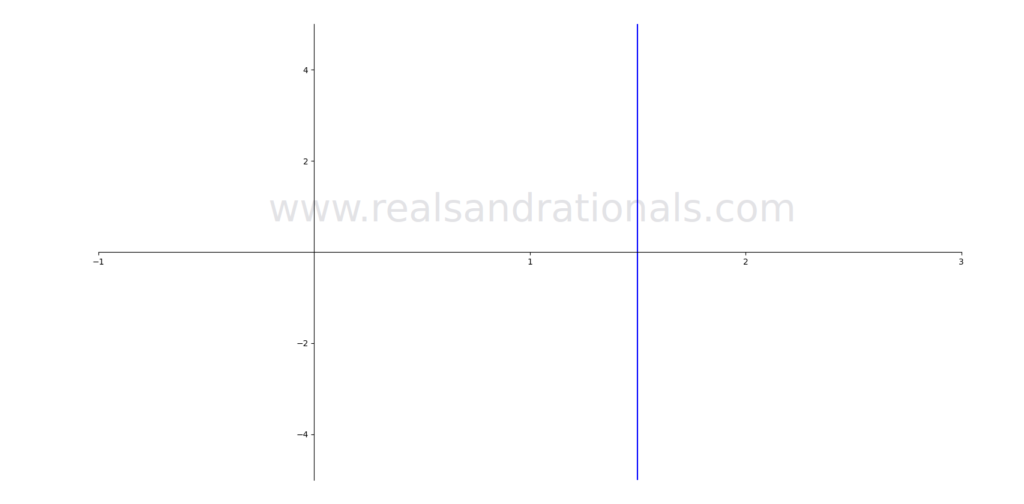
Which of the following graphs on the coordinate plane represent functions? If they are functions, identify their domain and range.






Problem set

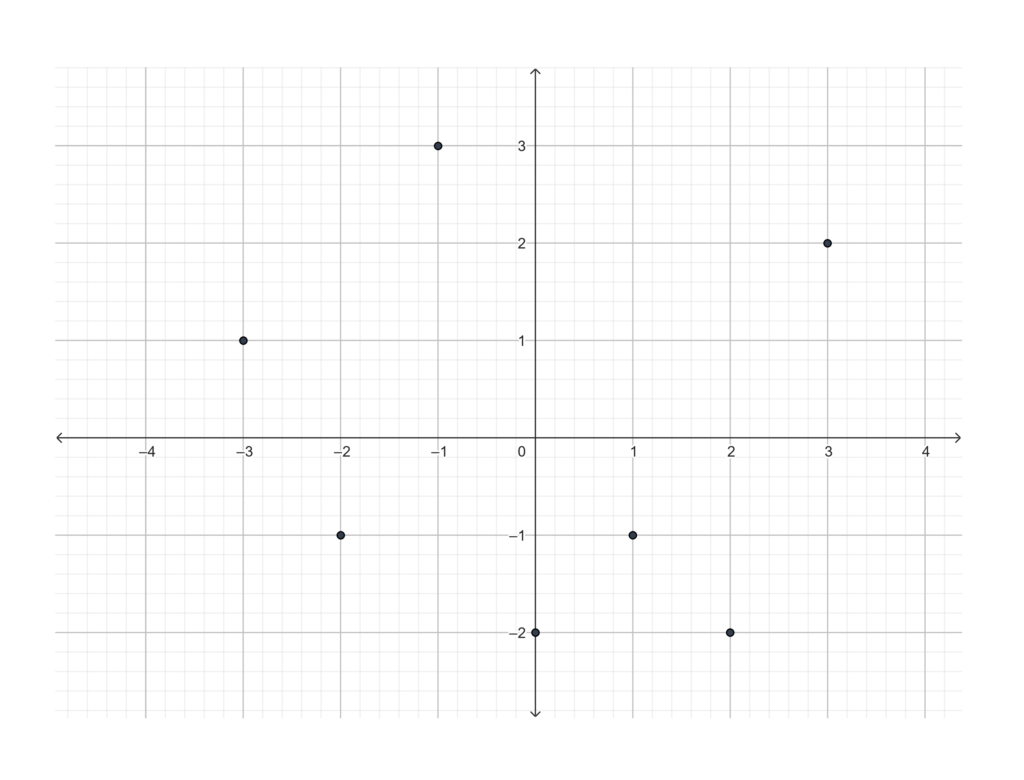
Which of the following graphs on the coordinate plane represent functions? If they are functions, identify their domain and range.







From representations as expressions

Exercises

Problem set

Identify the domain of each of the following functions.

  1. y = -x
  2. y = 2x+1
  3. y = 2x^2+5
  4. y = -2x^2-5x-5
  5. y = -2x^{100}-5x^{50}-5
Problem set

Identify the domain of each of the following functions.

  1. y = \frac{1}{x}
  2. y = \frac{3}{4x}
  3. y = \frac{1}{x+3}
  4. y = \frac{1}{2x+3}
  5. y = \frac{3x}{-2x-5}
  6. y = \frac{x^2}{-9x-6}
Problem set

Identify the domain of each of the following functions.

  1. y = \sqrt{x}
  2. y = \sqrt{x+3}
  3. y = 3x\sqrt{2x+3}
  4. y = \sqrt{-x}
  5. y = \sqrt{5-x}
  6. y = \sqrt{-3x-1}
  7. y = 8x\sqrt{-12x-6}
  8. y = -5x^2\sqrt{-5-4x}
Problem set

Identify the domains of the following functions.

  1. y = \sqrt[3]{x}
  2. y = (x+2)\sqrt{2}-(3x+1)\sqrt[3]{3}
  3. y = \frac{x^2}{5(3x-1)}
  4. y = x\sqrt{-3x-1}
Problem set

Identify the domains of the following functions.

  1. y = \frac{1}{\sqrt{x-5}}
  2. y = \sqrt{x^2+1}
  3. y = \frac{1}{\sqrt{x^2+1}}
  4. y = \frac{1}{(3x+1)(2x-5)}
  5. y = \frac{6x-5}{3x^2-8x+4}
  6. y = \frac{x^2+5x-6}{2x^2+13x+6}
Problem set

Identify the domains of the following functions.

  1. y = \sqrt{(x-1)(x-2)}
  2. y = \sqrt{(x-1)(x+2)}
  3. y = \sqrt{(3x+1)(2x-5)}
  4. y = \sqrt{18-x^2}
  5. y = \frac{1}{\sqrt{x^2-1}}
  6. y = \frac{x^2+1}{\sqrt{(x-1)(x+2)}}
  7. y = \frac{x}{\sqrt{3x^2-4x-4}}
  8. y = \frac{x}{\sqrt{|3x-4|}}
  9. y = \frac{x}{\sqrt{|3x-4|-5}}
Problem set

Which of the following equations represent functions? If they represent functions, identify their domain and range.

  1. y = 3
  2. y = |x|
  3. y = |x| - 3
  4. y = 2|x|
  5. x = |y|
  6. x = 3
Problem set

Which of the following equations represent functions? If they represent functions, identify their domain and range.

  1. y = |x-1|
  2. y = \sqrt{x+3}
  3. y = \sqrt{x}+3
  4. y = \frac{x+2}{x+1} (Challenge problem: find the range)
Problem set

Which of the following relations are functions? If they are functions, identify their domain.

  1. y = x^2
  2. y = \sqrt{x}
  3. y = \sqrt[3]{x}
  4. y = -3x-7
  5. 2x+4y-5=0
  6. 3x-4y-7=0

Set-theoretic formal definition

Exercises

Problem set

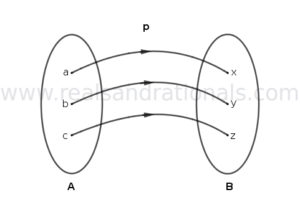
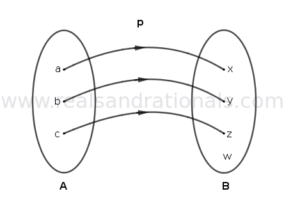
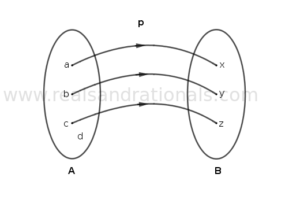
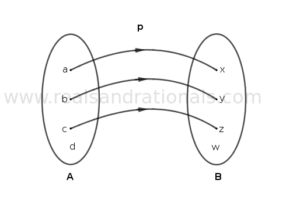
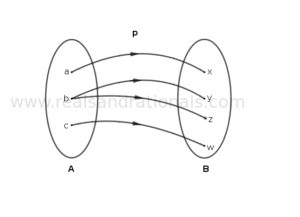
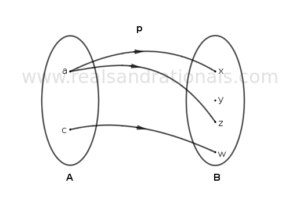
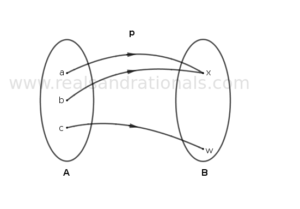
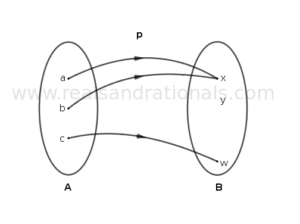
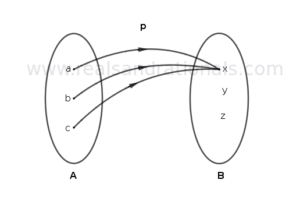
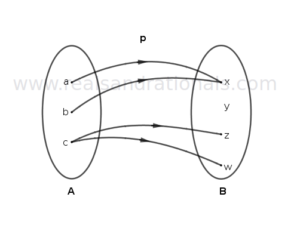
In each of the following figures, a relation between two sets of elements is shown. Determine if the relation is a function. If so, identify its domain, codomain and range, and write the function in notation showing its domain and codomain. If the relation is not a function, give the reason(s) why it is not.






Problem set

In each of the following figures, a relation between two sets of elements is shown. Determine if the relation is a function. If so, identify its domain, codomain and range, and write the function in notation showing its domain and codmain. If the relation is not a function, give the reason(s) why it is not.






Problem set

For each of the following, identify the domain, codomain and range.

  1. f:\mathbb{Z}\rightarrow\mathbb{Z} with f(x) = |x|
  2. f:\mathbb{Z}\rightarrow\mathbb{Q} with f(x) = x+1
  3. f:\mathbb{N}\rightarrow\mathbb{R} with f(x) = x-1
  4. f:\mathbb{R}\rightarrow\mathbb{R} with f(x) = 0
  5. f:\mathbb{Z}\rightarrow\mathbb{R} with f(x) = |x|+1

Problem set

For each of the following, identify the domain, codomain and range.

  1. f:\mathbb{W}\rightarrow\mathbb{R} with f(x) = x+10
  2. f:\mathbb{N}\rightarrow\mathbb{Z} with f(x) = -|x|
  3. f:\mathbb{R}\rightarrow\mathbb{R} with f(x) = |x|+2
  4. f:\mathbb{Q}\rightarrow\mathbb{R} with f(x) = -|x|
  5. f:\mathbb{R}\rightarrow\mathbb{R} with f(x) = \lfloor x \rfloor. Here, \lfloor x \rfloor denotes the greatest integer that is less than or equal to x. For example, \lfloor 3.12 \rfloor = 3, \lfloor -2.12 \rfloor = -3 and \lfloor -100 \rfloor = -100.

Problem set

Graph the following functions.

  1. f(x) = 2x, with domain \mathbb{N}
  2. g(x) = x^2, with domain \mathbb{Z}
  3. l(x) = \frac{x^2}{2}, with domain \mathbb{Z}
  4. h(x) = x-1, with domain \mathbb{Z}
  5. m(x) = x-1, with domain \mathbb{R}
  6. p(x) = -x+1, with domain \mathbb{Z}
  7. q(x) = -x+1, with domain \mathbb{R}
  8. s(x) = |x|, with domain \mathbb{Z}
  9. t(x) = |x|, with domain \mathbb{R}