Skip to content
Lesson notes
Lesson notes
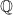 denotes the set of rational numbers, and
denotes the set of rational numbers, and 
- Between any two rational numbers, no matter how close they are, one can find another rational number. In fact, between any two rational numbers, one can find an infinite number of rational numbers.
- No matter how dense the rational numbers are on the number line, they do not completely fill up the number line. The number line still has holes
- Real numbers is the set of all numbers on the number line.
- Numbers that are real, but not rational – that is, numbers that cannot be expressed in the form
 where
where 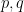 are integers and
are integers and  , are called irrational numbers.
, are called irrational numbers.
 is an example of irrational number.
is an example of irrational number.- If
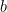 is an irrational number, then
is an irrational number, then 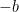 is also irrational.
is also irrational.
- If
 is rational (with
is rational (with  ) and
) and 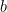 is irrational, then
is irrational, then  are all irrational.
are all irrational.
- If
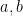 are both irrational, then
are both irrational, then  could be rational or irrational.
could be rational or irrational.
denotes the set of rational numbers, and
where
are integers and
, are called irrational numbers.
is an example of irrational number.
is an irrational number, then
is also irrational.
is rational (with
) and
is irrational, then
are all irrational.
are both irrational, then
could be rational or irrational.