AROC
Real-world interpretation
Exercises
Problem set
- The mean house price in a town was
in the year 2010, while the mean house price in the same town was
in the year 2020. Find the average rate of change of the mean house price in the town from 2010 through 2020.
- The cost of
pounds of rice is
, while the cost of
pounds of rick is
. Find the average rate of change of the cost of rice from
pounds of rice to
pounds of rice.
- A car consumed
gallons of gasoline to drive
miles, and the same car consumed
gallons of gasoline to drive
miles. Find the average rate of change of amount of gasoline consumed between driving
miles and driving
miles.
Problem set
- Chitra’s balance (in thousands of dollars) in her bank account is modeled by a function
, where
is time elapsed in years. Chitra observed that
. Give a layman’s interpretation of the AROC value for this real-world scenario.
- The population of a town is given by
, where
is the number of years elapsed from a certain date. If
, explain in layman’s language how the population of the town changed over time.
- A ball is thrown up into the air from the top of a building, and the height of the ball (in meters) from the ground is modeled by the function
, where
is time elapsed in seconds. It was observed that
. Give a layman’s interpretation of the AROC value for this real-world scenario.
- A truck drove from New York to Los Angeles. The distance driven by the truck as a function of time elapsed (in hours) is given by the function
. In the end, the truck took
hours to complete the drive and it was observed that
. Give a layman’s interpretation of the
.
- On a particular trip of length
miles, the gas remaining (in gallons) in the tank of a truck is modeled by the function
, where
gives the number of miles driven by the truck. If the truck consumed
gallon of gas for every
miles on average on the trip, give the value of
.
For functions as expressions
Exercises
Problem set
Find the AROC for the following functions in the interval .
Problem set
Find the AROC for the following functions in the interval .
For functions as graphs
Exercises
Problem set
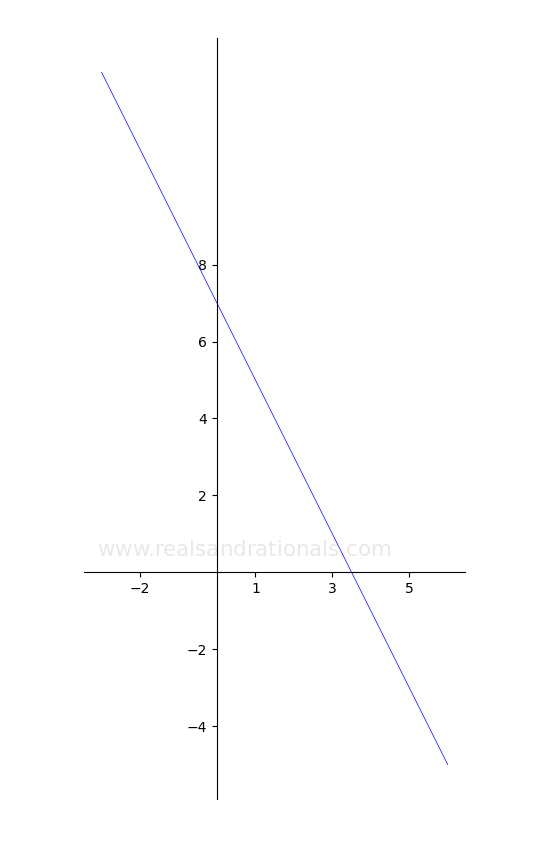
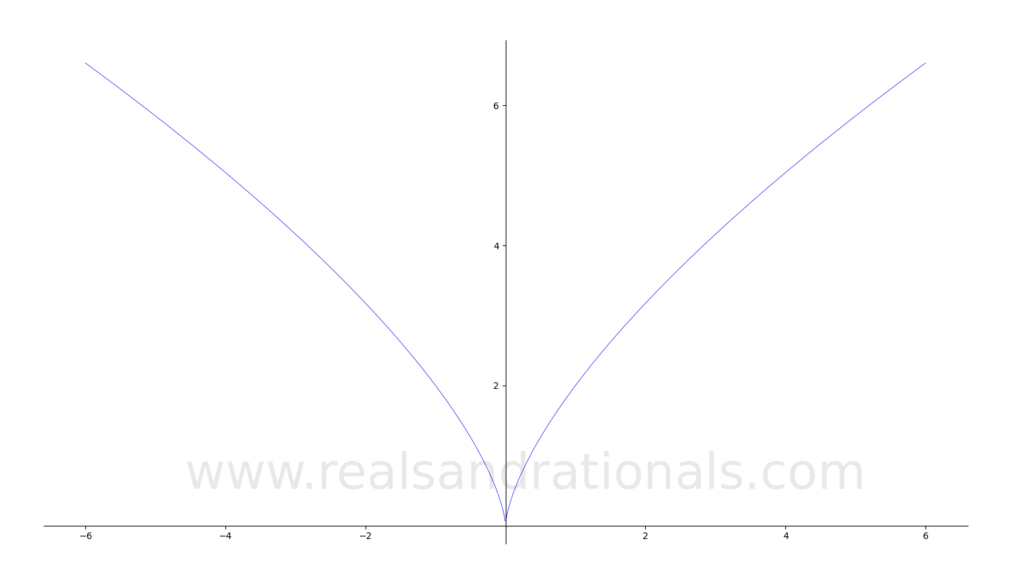
In each of the following problems, the graph of a function is shown. Using the graph, estimate the required AROC value.
Problem set
- For the following function
, identify which of the two is bigger:
.
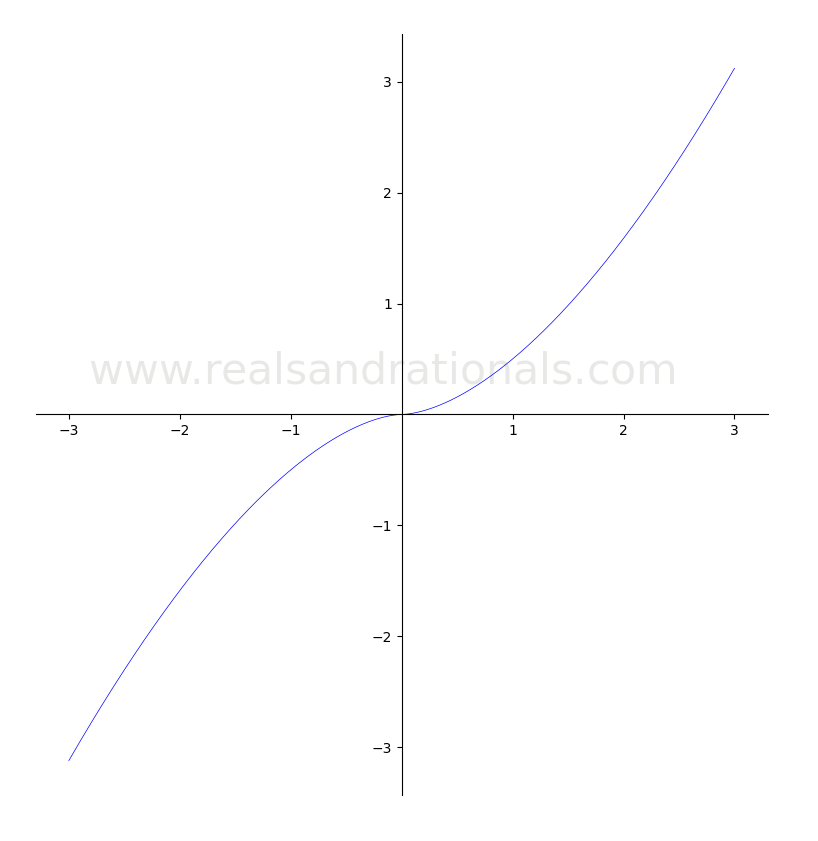
- For the following function
, arrange the following in ascending order:
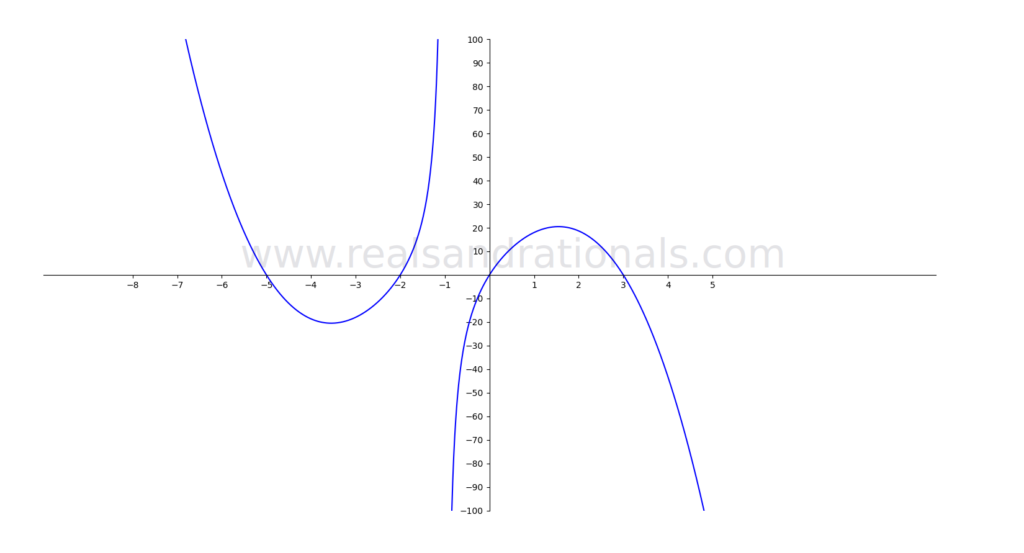
IROC
For functions as expressions
Exercises
Problem set
Find the IROC for the following functions using at two different points:
. Use calculators on this problem set.
For functions as graphs
Exercises
Problem set
In each of the following problems, the graph of a function is shown. Using the graph, estimate the required IROC value.
Problem set
- For the following function
, identify which of the two is bigger:
.

- For the following function
, arrange the following in ascending order:

- For the following function
, arrange the following in ascending order:
.
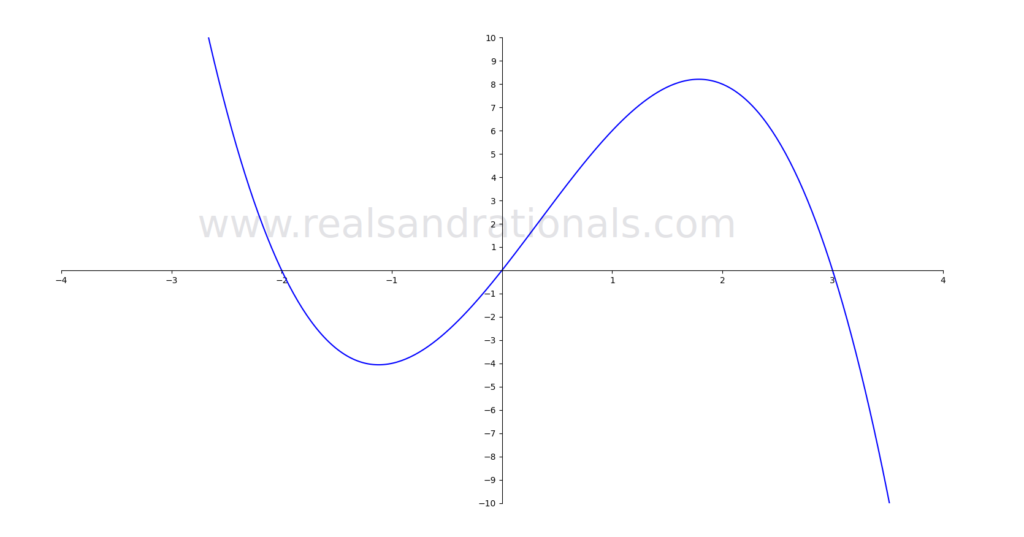
Problem set
-
In each of the following problems, certain AROC and IROC values of a function
-
-
-
Natural base of an exponential function
Exercises
Problem set
Using , find the IROC for the following functions using
at the three different points:
. Use calculators on this problem set.
Problem set
Problems requiring where IROC is proportional to function value (Heat transfer, Newton’s law of cooling?)