Learn – Algebra/Precalculus – Functions

Inverse

Motivation

Exercises

Problem set
  1. A function that takes number of apples as input and gives cost as output is given by y = 0.75x + 0.1. Give the expression for the related function that gives the number of apples that can be purchased as output taking the number of dollars as input.
  2. John’s balance in his bank account as a function of number of years elapsed since 2018 is given by y = 50000 + 24000x. Give the expression of a function that gives number of years required for a certain target bank balance.
  3. A truck leaves from New York City to Los Angeles. The amount of gas (in gallons) left in the tank of the truck as a function of number of miles driven is given by y = 200 - 0.1x. Since the truck does not have a trip meter, and the driver wants to estimate the miles driven based on the amount of gas left in the tank. Give an equation for a function that helps the driver estimate the miles driven based on the amount of gas left in the tank.
  4. The height of a ball from the ground as a function of time is given by y = -2x^2 + 500. Give the expression for the function that gives time elapsed when the ball is at a certain height.
  5. A radio active substance has a mass of 1050g as measured at 8:00AM on July 1st, 2020. The mass of the substance as a function of number of hours that elapsed since the initial measurement is modeled by the function y = 1000\times 0.95^x. Give the function that models the number of hours elapsed when the mass of the substance is known.
  6. The population of a town as a function of number of years that elapsed since 2010 is modelled by the function y = 73000\times 1.08^x. Give the function that models the year given a certain population for the town.

Equations

Exercises

Problem set

Find the inverses for each of the following functions.

  1. f(x) = 7x + 3
  2. g(x) = -9x - 1
  3. l(x) = -4x + 5
  4. h(x) = x^5
  5. t(x) = 3x^5-7
Problem set

Find the inverses for each of the following functions.

  1. l(x) = \frac{3x^3-5}{7}
  2. t(x) = \frac{1}{3x-7}
  3. h(x) = \frac{3}{5x^3-9}
  4. g(x) = \frac{5}{7-5x^4}
  5. f(x) = \frac{3}{2-3x^5}
Problem set

Find the inverses for each of the following functions.

  1. r(x) = 2^x
  2. l(x) = 4^x+5
  3. p(x) = 3\times5^x-4
  4. q(x) = -5\times3^x-7
  5. h(x) = e^x
  6. f(x) = e^{2x-5}
  7. g(x) = 5e^{-7x+3}-8
  8. t(x) = 4\sqrt{e^{-3x+1}-2}
Problem set

Find the inverses for each of the following functions.

  1. y = \log^{x}_3
  2. y = \log^{x}_5 - 3
  3. y = 2\log^{x}_7 + 4
  4. y = \log^{(x+5)}_4
  5. y = \ln (x+5)
  6. y = 2\times3^{4x^2+5}+6
  7. y = 3\times3^{\sqrt{x+1}}-6
  8. y = 5\ln (x^2+5)
  9. y = 7\ln \sqrt{x-1}
  10. y = \sin (2x+5)
  11. y = 3\tan (2x+5)-4
Problem set

Notation for certain well-known sets is used as follows.

  • \mathbb{N} – Set of Natural numbers
  • \mathbb{Q} – Set of Rational numbers
  • \mathbb{Z} – Set of Integers
  • \mathbb{W} – Set of Whole numbers
  • \mathbb{R} – Set of Real numbers

Which of the following functions have inverses?

  1. f:\mathbb{Z}\rightarrow\mathbb{Z} with f(x) = |x|
  2. f:\mathbb{Z}\rightarrow\mathbb{Q} with f(x) = x+1
  3. f:\mathbb{W}\rightarrow\mathbb{R} with f(x) = x+1
  4. f:\mathbb{N}\rightarrow\mathbb{W} with f(x) = x-1
  5. f:\mathbb{R}\rightarrow\mathbb{R} with f(x) = 0
Problem set

In this problem set, we follow the same notations as in the previous problem set.

  1. Function f is defined as: f:\mathbb{Z}\rightarrow\mathbb{Z} with f(x) = x^3. Does f have an inverse?
  2. Function f is defined as: f:\mathbb{Z}\rightarrow\mathbb{Z} with f(x) = -x. Does f have an inverse?
  3. Let A = \mathbb{Q}-\{0\}. I have a relation \rho from set A to set A given by \rho(x) = \frac{1}{x}. Is \rho a function? If so, does \rho have an inverse?
Problem set

Which of the following functions have inverses? Assume the domain is \mathbb{R} unless stated otherwise.

  1. f(x) = |x|
  2. g(x) = x^3
  3. h:\mathbb{R}^+\rightarrow \mathbb{R}, h(x) = x^2. \mathbb{R}^+ denotes the set of positive real numbers.
  4. t(x) = 7x+3
  5. t(x) = 0

Graphing

Exercises

Problem set

In each of the following, the graph of a function is shown. For each one, graph the inverse.






















Problem set

Which of the following functions have inverses?






Set pairing diagrams

Exercises

Problem set

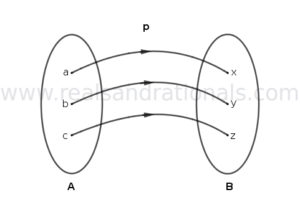
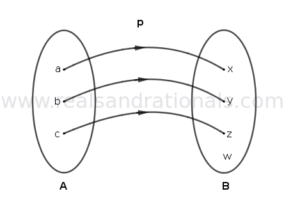
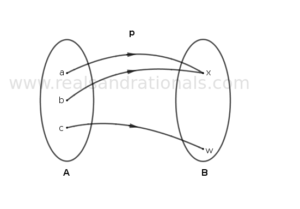
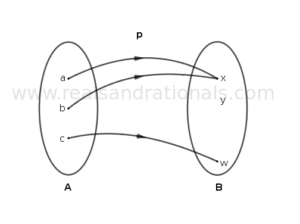
For each of the following problems, answer if the function shown has an inverse. If inverse exists, represent the inverse in a function diagram.






Even functions, odd functions

Exercises

Problem set

  1. Is this function even, odd or neither: 4x^9-8x^3+2x
  2. Evaluate: \cos \theta for \theta = -2\pi,-\frac{11\pi}{6},-\frac{10\pi}{6}, -\frac{3\pi}{2},-\frac{8\pi}{6},-\frac{7\pi}{6},-\pi,-\frac{5\pi}{6},-\frac{4\pi}{6},-\frac{\pi}{2},-\frac{\pi}{3},-\frac{\pi}{6}, 0, \frac{\pi}{6}, \frac{\pi}{3}, \frac{\pi}{2}, \frac{4\pi}{6}, \frac{5\pi}{6}, \pi, \frac{7\pi}{6}, \frac{8\pi}{6},\frac{3\pi}{2},\frac{10\pi}{6},\frac{11\pi}{6},2\pi. Using the values as a guide, plot \cos x on the coordinate plane for -2\pi \le x \le 2\pi. From the graph, does \cos (x) appear to be an odd function or even function?
  3. Evaluate: \sin \theta for \theta = -2\pi,-\frac{11\pi}{6},-\frac{10\pi}{6}, -\frac{3\pi}{2},-\frac{8\pi}{6},-\frac{7\pi}{6},-\pi,-\frac{5\pi}{6},-\frac{4\pi}{6},-\frac{\pi}{2},-\frac{\pi}{3},-\frac{\pi}{6}, 0, \frac{\pi}{6}, \frac{\pi}{3}, \frac{\pi}{2}, \frac{4\pi}{6}, \frac{5\pi}{6}, \pi, \frac{7\pi}{6}, \frac{8\pi}{6},\frac{3\pi}{2},\frac{10\pi}{6},\frac{11\pi}{6},2\pi. Using the values as a guide, plot \sin x on the coordinate plane for -2\pi \le x \le 2\pi. From the graph, does \sin (x) appear to be an odd function or even function?

Problem set

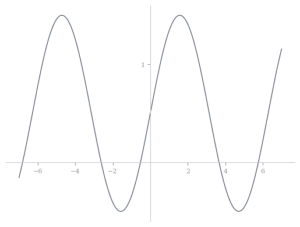
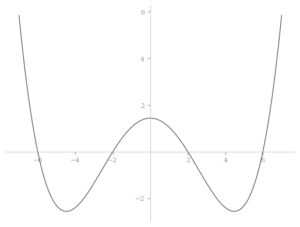
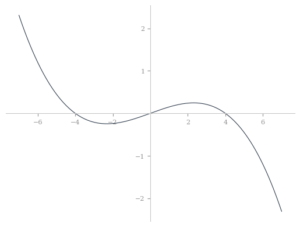
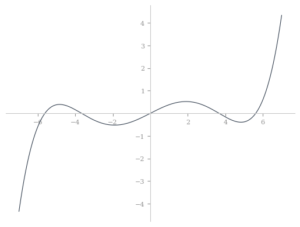
Identify if each of the following functions graphed below is even, odd or neither.








Problem set

A function f:\mathbb{R}\to\mathbb{R} is called even if f(-x) = f(x) for all x.
A function g:\mathbb{R}\to\mathbb{R} is called odd if g(-x) = -g(x) for all x.

Use the above definitions to determine if the following functions are even, odd or neither.

  1. x^4-x^2+x+1
  2. -5x^6+3x^4-7x^2+9
  3. \frac{5x^4-3x^2-1}{-5x^6+3x^4-7x^2+9}
  4. \frac{5x^3-3x^5-0.5x}{7x^5+3x^7-8x^9}
  5. \frac{5x^3-3x^5-0.5x}{-7x^6+3x^8-8x^{10}}

Problem set

Use the definitions in the previous problem set to determine if the following functions are even, odd or neither.

  1. \sin x
  2. \cos x
  3. \tan x
  4. \csc x
  5. \sec x
  6. \cot x

Problem set

Determine if the following functions are even, odd or neither.

  1. \cos x - \sec x
  2. \sin x + \cos x
  3. \tan x - \cot x

Problem set

Determine if the following functions are even, odd or neither.

  1. (5x^5-7x^3-9x)^4
  2. (4x^6+6x^4+9x^2)^3
  3. 3\sin x^2\tan x^2
  4. 3\sin^2 x\tan^2 x
  5. \frac{e^x+e^{-x}}{2}
  6. \frac{e^x-e^{-x}}{2}

Compositions

Exercises

Problem set

  1. A marathoner consumes a tenth of a gallon of water for every mile that he runs. The cost of a gallon of water is half-a-dollar.
    1. Give a function g(m) that models the gallons consumed by a marathoner that runs m miles.
    2. Give a function c(g) that models the cost incurred as g gallons of water are consumed.
    3. Give the function composition e(m) = c\left(g(m)\right) that estimates the cost of water for a marathoner that runs m miles.
  2. Prof.Benedetto starts an experiment in his lab with 1000 bacteria. The bacteria is expected to double in population every 3 weeks. A lab dish in the lab can accommodate 10000 bacteria.
    1. Give a function p(w) that models the population of the bacteria after w weeks have elapsed.
    2. Give a function d(p) that models the number of lab dishes that are required to house p bacteria.
    3. Give the function composition l(w) = d\left(p(w)\right) that estimates the number of lab dishes that are required to house the bacteria in Prof.Benedetto’s experiment after w weeks.

Problem set

In each of the following cases, claim if g\circ f is defined. If g\circ f is defined, identify its domain and codomain.

  1. f:A\to B, g:B\to C
  2. g:A\to B, f:B\to C
  3. f:A\to B, g:B\to A
  4. f:\mathbb{R}\to \mathbb{Z}, g:\mathbb{R}\to \mathbb{Z}
  5. f:\mathbb{R}\to \mathbb{R}, g:\mathbb{R}\to \mathbb{R}

Problem set

  1. If f and g are two functions with domains \{1,2,3\} and \{a,b,c\} respectively. And, f(1) = a, f(2) = a, f(3) = b and g(a) = \gamma, g(b) = \alpha, g(c) = \gamma. Find the values of the following if they are defined:
    1. (g\circ f)(1)
    2. (g\circ f)(3)
    3. (f\circ g)(a)
    4. (f\circ g)(1)
  2. If f and g are two functions such that f:\{1,2,3\}\to \{1,2,3\}, f(1) = 3, f(2) = 2, f(3) = 1 and g:\{1,2,3\}\to \{1,2,3\}, g(1) = 3, g(2) = 2, g(3) = 1, find the values of the following if they are defined:
    1. (g\circ f)(1)
    2. (g\circ f)(2)
    3. (f\circ g)(3)
    4. (f\circ g)(1)
    5. (f\circ g)(2)
    6. (f\circ g)(3)

Problem set

Find expressions for (f\circ g)(x) and (g\circ f)(x) for each of the following.

  1. f(x) = 2x+1, g(x) = \sqrt{x}
  2. f(x) = 2x+1, g(x) = \frac{x-1}{2}
  3. f(x) = x^2-2, g(x) = 3^x
  4. f(x) = 2^x, g(x) = \log^x_2
  5. f(x) = e^x, g(x) = \ln x

Problem set

Find expressions for (f\circ g)(x) for each of the following.

  1. f(x) = (x-1)^{2/3}, g(x) = x^{3/2}+1
  2. f(x) = e^{\sqrt{3x+9}}, g(x) = \frac{(x+3)(x-3)}{3}
  3. f(x) = 2x^2-1, g(x) = \cos \left(\frac{x}{2}\right)
  4. f(x) = \frac{x}{3}, g(x) = \ln (ex)^3

Problem set

For each of the following, identify two composing functions that make up given function.

  1. \ln(2x^2+3x+1)
  2. \sqrt{e^x+1}
  3. \sin(\cos x)
  4. \sin x^7
  5. \sin^7 x

Problem set

For each of the following, identify two composing functions that make up given function.

  1. e^{\sin x}
  2. e^{x^5+3x^2+1}
  3. (3x^2+5x+9)^{53}
  4. (4-7x^5+5x^9)^{93}
  5. 5(3x-4)^3-9(3x-4)^2+4(3x-4)-1
  6. 2\sin^2 x+3\sin x+1

Problem set

For each of the following, identify three composing functions that make up given function.

  1. \sqrt{\sin^2 x + 3}

Recursive functions

Exercises

Problem set

In each of the following scenarios, give a recursive expression for the function.

  1. Anna-marie had opened a bank account with a balance of \$10000. From then on, she deposited \$1500 every month into her account. The function a(m) models her account balance at the end of month m.
  2. Big hearts child care center charges \$100 for registration. The monthly cost for the care of a single child at the center is \$ 800. The function c(m) models the total cost incurred by a family after having their child in the center for m months.
  3. Dr.Moriarty is doing an experiment with bacteria in his lab. He started with a bacteria population of 200000. He observes that the bacteria population is doubling every minute.The function p(t) models the population after t minutes have elapsed.
  4. The first time census was taken for an island in Estonia, its population was 66000. Every year since, the population has been multiplying by a factor 1.02. The function e(y) models the population of the town after y years.
  5. The first time census was taken for a town in Madagascar, its population was 78000. Every year since, the population has been increasing by 1\%. The function m(y) models the population of the town after y years.

Problem set

In each of the following scenarios, give a recursive expression for the function.

  1. Anna-marie had opened a bank account with a balance of \$10000. From then on, she deposited \$3000 every two months into her account. The function a(m) models her account balance at the end of month m.
  2. Mr.Magruder is doing an experiment with bacteria in his lab. He started with a bacteria population of 200000. He observes that the bacteria population is doubling every three minutes.The function p(t) models the population after t minutes have elapsed.
  3. The first time census was taken for a town in Sri Lanka, its population was 36000. The census was taken of the town once every three years since then. It was observed that the population increased by 3\% each time. The function m(y) models the population of the town after y years.

Problem set

Explain what happens in each of the following function models expressed recursively.

  1. c(0) = 100, c(w+1) = c(w) + 20
  2. a(0) = 2000, a(m+1) = a(m) + 200
  3. b(0) = 2000, b(m+1) = 2b(m)
  4. p(0) = 12345, p(t+1) = 1.03p(t)

Problem set

Explain what happens in each of the following function models expressed recursively.

  1. c(0) = 500, c(w+2) = c(w) + 100
  2. a(0) = 2000, a(m+3) = a(m) + 1000
  3. b(0) = 2000, b(m+3) = 2b(m)
  4. p(0) = 12345, p(t+5) = 0.5p(t)

Problem set

Give the explicit expressions for each of the following functions expressed recursively.

  1. c(0) = 100, c(w+1) = c(w) + 20
  2. a(0) = 2000, a(m+1) = a(m) - 200
  3. b(0) = 100, b(w+3) = b(w) + 20
  4. b(0) = 100, b(w+3) = b(w) - 20

Problem set

Give the explicit expressions for each of the following functions expressed recursively.

  1. p(0) = 3, p(m+1) = 2p(m)
  2. q(0) = 2000, q(m+1) = 0.5q(m)
  3. r(0) = 3, r(t+3) = 2r(t)
  4. s(0) = 200, s(t+5) = 0.5s(t)

Problem set

Give the recursive expressions for each of the following functions expressed explicitly.

  1. a(x) = 2x+1
  2. b(x) = \frac{x}{2}+100
  3. c(x) = 2x-100
  4. d(x) = -2x+100
  5. e(x) = -\frac{x}{2}-100

Problem set

Give the recursive expressions for each of the following functions expressed explicitly.

  1. p(x) = 2\times 2^x
  2. q(x) = -2\times 2^x
  3. r(x) = 200\times \left(\frac{1}{2}\right)^x
  4. s(x) = 10\times 4^{x/6}
  5. t(x) = 200\times \left(\frac{1}{2}\right)^{x/20}