Learn – Calculus – Applications of Definite Integrals

Areas and volumes of regular figures

Exercises

Problem set

In each of the following, assume that you do not have a formula to calculate the required quantity.

  1. Express the area of a semicircle of radius r as a definite integral. Use the division strategy of dividing the semicircle into vertical sections.
  2. Express the area of a circle of radius r as a definite integral. Use the division strategy of dividing the circle into concentric rings.
  3. Express the area of a circle of radius r as a definite integral. Use the division strategy of dividing the circle into sectors.
  4. Express the volume of a hemisphere of radius r as a definite integral.
  5. Express the volume of a cone, whose base has radius r and whose height is h, as a definite integral.
  6. Express the volume of a square pyramid, whose base has side length s and whose height is h, as a definite integral.

Areas enclosed by curves

Exercises

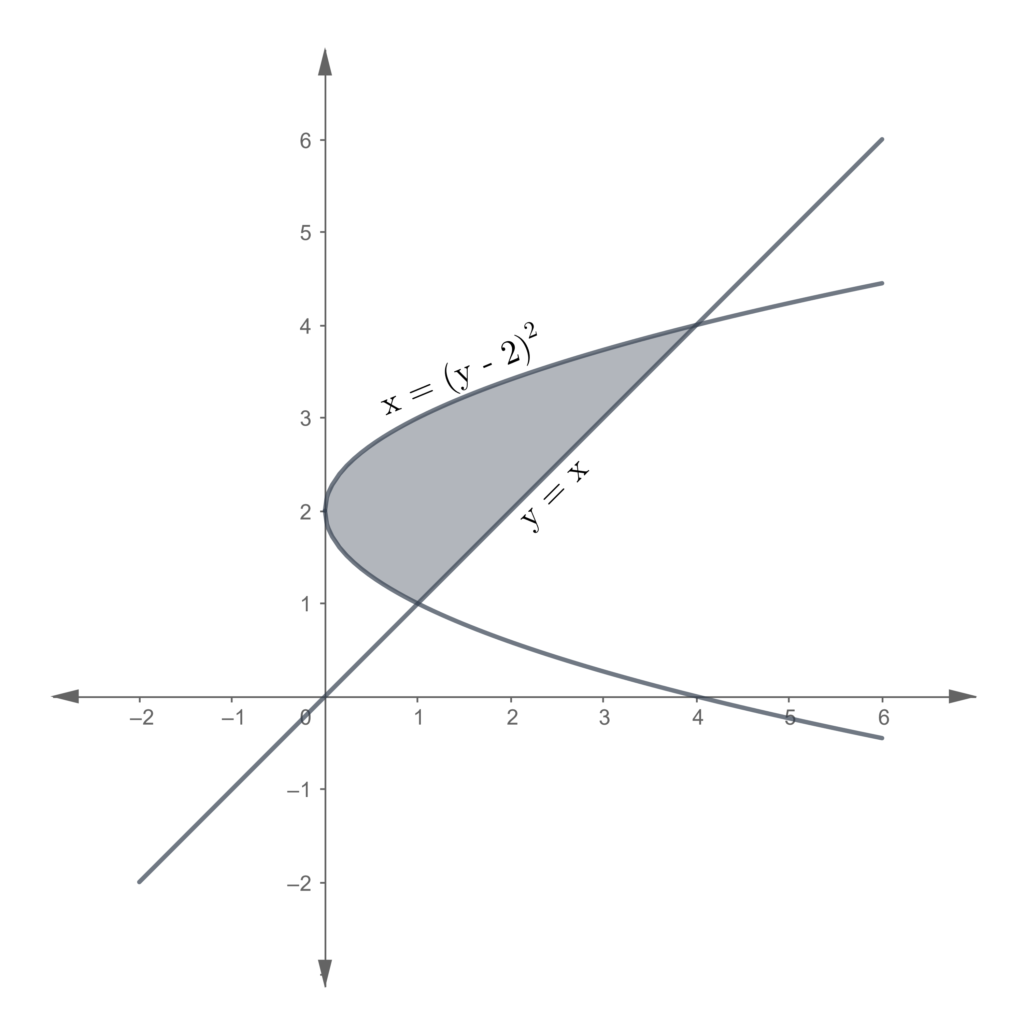
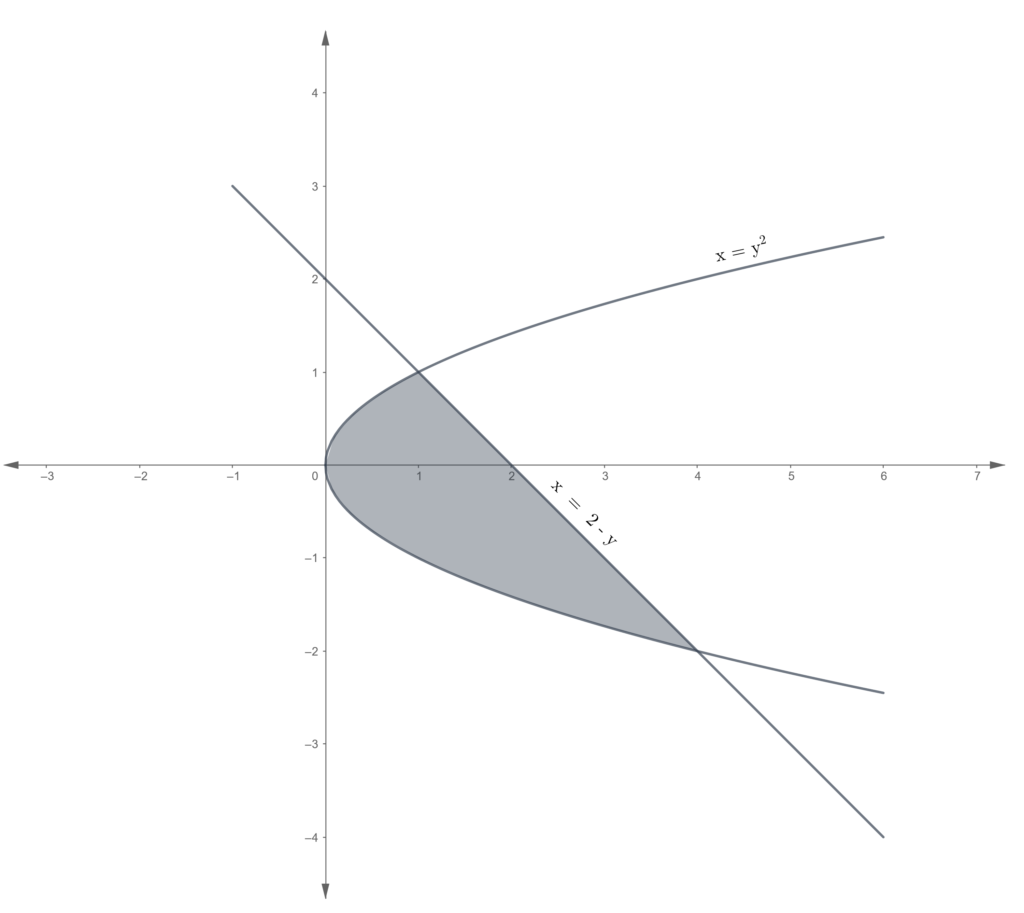
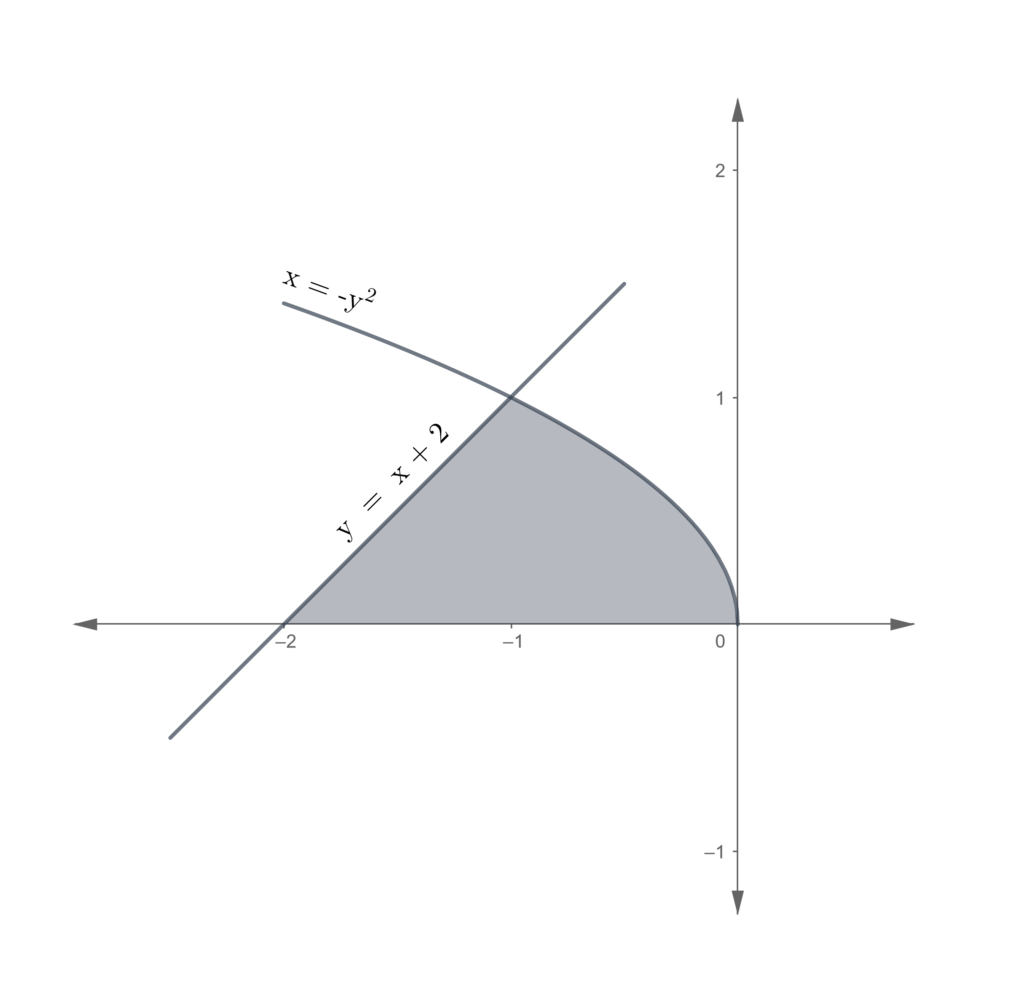
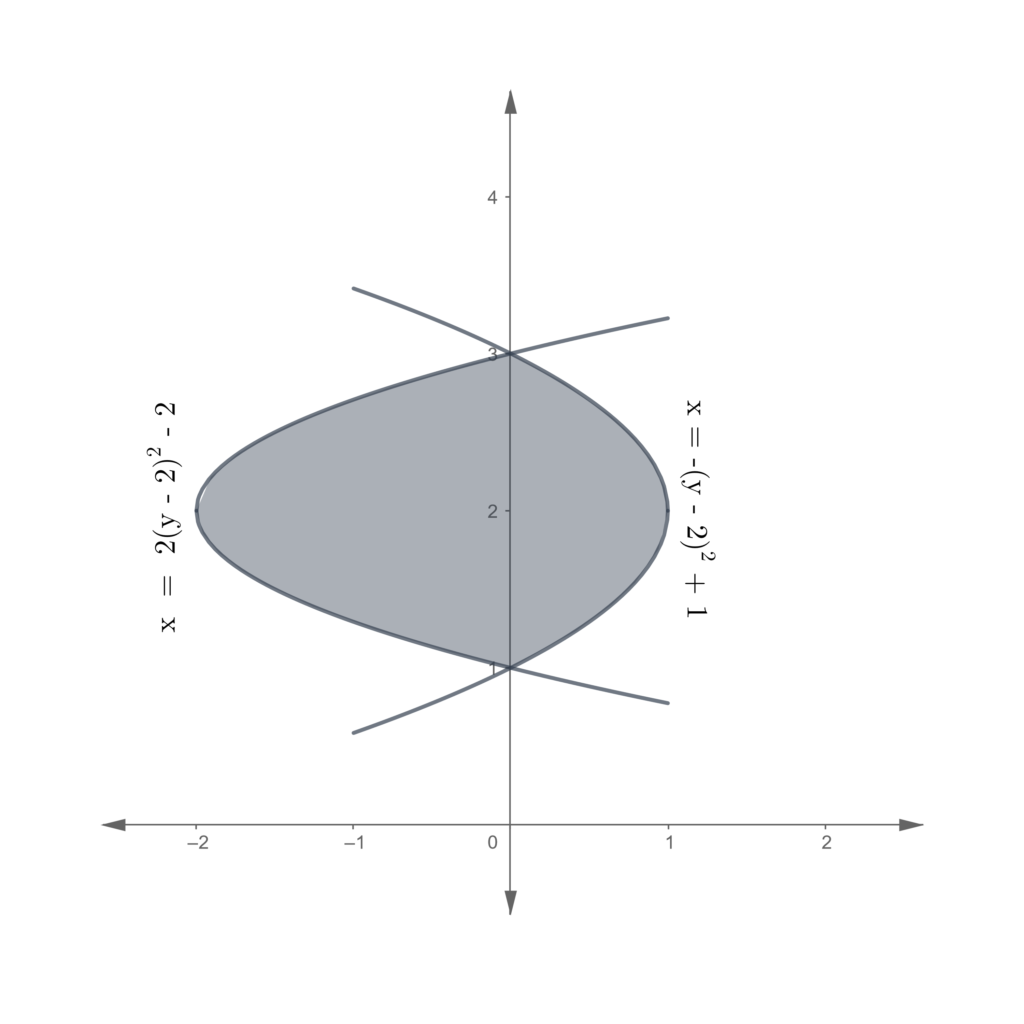
Problem set

In each of the following problems, find the area of the region enclosed.

  1. y = x^2, x=-2, x=2, y=0
  2. y = \cos x, x=-\frac{\pi}{2}, x=\frac{\pi}{2}, y=0
  3. y = \frac{1}{x}, x=1, x=e, y=0
  4. y = \sec^2 x, x=-\frac{\pi}{4}, x=\frac{\pi}{4}, y=0
  5. y = \tan^2 x, x=-\frac{\pi}{4}, x=\frac{\pi}{4}, y=0

Problem set

In each of the following problems, find the area of the region enclosed.

  1. y = 2(x-3)^2+1, x=2, x=4, y=0
  2. y = (x-3)(x+1), x=-1, x=2, y=0
  3. y = \frac{4}{x+1}, y = x-2, x=0

Problem set

In each of the following problems, find the area of the region enclosed.

  1. y = \sin x, x=\frac{\pi}{3}, x=\frac{2\pi}{3}, y=\frac{1}{\sqrt{2}}
  2. y = \cos x, x=-\frac{\pi}{4}, x=\frac{\pi}{4}, y=1
  3. y = (x-2)(x+2), x=-3, x=3, y=6

Problem set

In each of the following problems, find the area of the region enclosed.

  1. y = x, y=x^2
  2. y = x^2, y=x^3
  3. y = \sqrt{x}, y=x^3
  4. y = x^2-2, y = 2-x^2
  5. y = (x-2)^2+1, y=-(x-3)^2+2

Problem set

In each of the following problems, find the area of the region between the curves given.

  1. y = \sin x, y = \cos x, 0\le x\le \frac{\pi}{4}
  2. y = \sin^2 x, y = 2\sin x, 0 \le x \le \pi
  3. y = \sin x, y = \csc^2 x, \frac{\pi}{4} \le x\le \frac{3\pi}{4}
  4. y = \cos^2 x, y = 2\cos x, \frac{\pi}{2} \le x \le \frac{3\pi}{2}
  5. y = \cos x, y = \sec^2 x, \frac{3\pi}{4} \le x \le \frac{5\pi}{4}

Problem set

In each of the following problems, find the area of the region enclosed.

  1. y = e^x, y = 2x+2, 0 \le x \le 1
  2. y = e^x, y = (e-1)x+1

Problem set

In each of the following problems, find the area of the region enclosed.

  1. x = (y-4)^2, x = 2.
  2. x = y^2 - 2, x = 2 - y^2.
  3. y = \sqrt{2x}, x+y = 4

Problem set

In each of the following problems, find the area of the shaded region.





Volumes of solids of revolution

Exercises

Problem set

For each of the following, find the volume of the solid obtained by revolving the given curve about the given axis of revolution.

  1. y = x^2,\,2 \le x \le 5, \mbox{ Axis of revolution: }X\mbox{-axis}
  2. y = \sqrt x,\,0 \le x \le 4, \mbox{ Axis of revolution: }X\mbox{-axis}
  3. y = \frac{r}{h}x,\,0 \le x \le h, \mbox{ Axis of revolution: }X\mbox{-axis}
  4. y = x^2,\,1 \le x \le 2, \mbox{ Axis of revolution: }Y\mbox{-axis}
  5. y = \ln x,\,1 \le x \le e, \mbox{ Axis of revolution: }Y\mbox{-axis}

Problem set

For each of the following, find the volume of the solid obtained by revolving the region between the two curves about the given axis of revolution.

  1. y = \sqrt{x},\, y=\frac{1}{x^2}, \, 1 \le x \le 4, \mbox{ Axis of revolution: }X\mbox{-axis}
  2. y = x,\,y=x^2, \mbox{ Axis of revolution: }X\mbox{-axis}
  3. y = \sin x,\, y=\cos x, \, \frac{\pi}{4} \le x \le \frac{\pi}{2}, \mbox{ Axis of revolution: }X\mbox{-axis}
  4. y = x^2,\,y=x, \mbox{ Axis of revolution: }Y\mbox{-axis}
  5. y = \sqrt{x},\,y=x^3, \mbox{ Axis of revolution: }x=5
  6. y = \ln x, \, y = \frac{x-1}{e-1},\, 1\le x\le e, \mbox{ Axis of revolution: }x=-1

Problem set

For each of the following, find the volume of the solid obtained by revolving the region bounded as specified about the given axis of revolution.

  1. y = -x^2+4x,\, 0 \le x \le 4, \mbox{ Axis of revolution: }Y\mbox{-axis}
  2. y = \frac{\sin x}{x},\, 0 < x \le \pi, \mbox{ Axis of revolution: }Y\mbox{-axis}
  3. y = \frac{\sin x}{x},\, -\pi \le x \le \pi, \mbox{ Axis of revolution: }x = 4

Curve lengths and surface areas of solids of revolution

Exercises

Problem set

  1. Assume f(x) is a function whose derivative f'(x) is continuous. Express the length of the curve y=f(x) from x=a through x=b as a definite integral. Derive (jusitfy) your expression.
  2. Assume f(x) is a function whose derivative f'(x) is continuous in [a,b]. Express the surface of the solid generated by revolving y = f(x) about the X-axis as a definite integral. Derive (jusitfy) your expression.
  3. Find the length of the curve y = \frac{2}{3} x^{3/2}, 0 \le x \le 1.
  4. Find the volume of the solid obtained by revolving y=\sqrt{x}, 0\le x \le 1 about the the X-axis.

Acceleration, Velocity and Distance

Exercises

Problem set

  1. Assume velocity of a particle as a function of time is given by the functions \frac{1}{2}t^2+2t+5.

    1. Express the distance traveled by the particle between time units 10 and 100 approximately as a Riemann sum.
    2. Express the distance as a definite integral.
  2. The velocity of an object moving along X-axis is given by v(t) = 3t^2-4t+1, where t is time in seconds. The object is at x = 2 initially.

    1. Model the displacement of the object from its initial position as a Riemann sum.
    2. Determine the object’s position after 4 seconds.
  3. The velocity of an object moving along X-axis is given by v(t) = t-4, where t is time in seconds. The object is at x = 1 initially.

    1. Model the displacement of the object from its initial position as a Riemann sum.
    2. Determine the object’s position after 6 seconds.
    3. Model the total distance traveled by the object as a Riemann sum.
    4. Determine the distance traveled by the object in 8 seconds.
  4. The velocity of an object moving along X-axis is given by v(t) = |t-2|-1, where t is time in seconds. The object is at x = 1 initially.

    1. Model the displacement of the object from its initial position as a Riemann sum.
    2. Determine the object’s position after 6 seconds.
    3. Model the total distance traveled by the object as a Riemann sum.
    4. Determine the distance traveled by the object in 4 seconds.
  5. The velocity of an object moving along X-axis is given by v(t) = \csc^2 \left(t+\frac{\pi}{4}\right) - 1, where t is time in seconds. The object is at x = 1 initially.

    1. Model the displacement of the object from its initial position as a Riemann sum.
    2. Determine the object’s position after \frac{\pi}{2} seconds.
    3. Model the total distance traveled by the object as a Riemann sum.
    4. Determine the distance traveled by the object in \frac{\pi}{2} seconds.
  6. The velocity of an object moving along X-axis is given by v(t) = \pi\sqrt{2}\sin \pi (t+0.25), where t is time in seconds. The object is at x = -1 initially.

    1. Model the displacement of the object from its initial position as a Riemann sum.
    2. Determine the object’s position after 3.5 seconds.
    3. Model the total distance traveled by the object as a Riemann sum.
    4. Determine the distance traveled by the object in 4 seconds.

Problem set

  1. The acceleration of an object moving along X-axis is given by a(t) = 2t, where t is time in seconds. The object’s initial position and initial velocity are x = 1 and 3 meter per second respectively.
    1. Model the velocity of the object as a Riemann sum.
    2. Determine the object’s velocity after 2 seconds.
    3. Determine the object’s position after 4 seconds.
  2. The acceleration of an object moving along X-axis is given by a(t) = t-4, where t is time in seconds. The object’s initial position and initial velocity are x = 1 and -2 meter per second respectively.
    1. Model the velocity of the object as a Riemann sum.
    2. Determine the object’s velocity after 8 seconds.
    3. Determine the object’s position after 8 seconds.

Problem set

  1. Velocity graphs
  2. Assume the acceleration because of gravity is 9.8 \mbox{m/sec}^2. If an object is dropped from a building of height 196\mbox{m}, how long would the object take to hit the ground?
  3. Assume the acceleration because of gravity is 9.8 \mbox{m/sec}^2. If an object thrown into the air from the top of a building of height 196\mbox{m} with an initial velocity of 1.9\mbox{m/sec},
    1. What is the maximum height that the object reaches?
    2. What is the time it takes for the object to hit the ground?