Learn – Calculus – Applications of Derivatives

Increasing and Decreasing functions

Problem set

In each of the following problems, give whether the function $f(x)$ goes up or down at the given $x$ value.

At $x=2$ , if $f'(2) = 5$
At $x=-5$ , if $f'(-5) = 0.2$
At $x=4$ , if $f'(4) = -0.5$
At $x=0$ , if $f'(0) = -3$
At $x=7$ , if $f'(4) = -0.4$
At $x=5$ , if $f'(5) = 0$

Problem set

In each of the following problems, give whether the given function goes up or down at the given $x$ value.

$f(x) = x^3+x^4$ at $x=-2$
$f(x) = x^4-x^6$ at $x=-0.1$

Problem set

In each of the following problems, identify the intervals where the function is increasing and decreasing.

$5x^2+4x+7$
$12x^3-4x$
$x^3-x^2-5x+7$

Minima and maxima

Problem set

For each of the following problems, graph the given function (approximately) and estimate where the extreme values of the function occur. Using calculus, find where the extreme values actually occur.

$x^3-4x$
$(x-1)(x+1)(x+5)$
$\frac{x}{x^2+2x+3}$
$\sin x + \cos x$ in $[0, 2\pi]$
$2\sin x - x$ in $[0, 2\pi]$

Problem set

For each of the following functions, identify the intervals where the function increases, the intervals where the function decreases, the local extreme values and the absolute extreme values.

$16x^4-1$
$2x^3-4x^2+2x+7$
$2(x-1)^6-5$
$-3(3x+2)^4+7$
$3x^3-5$

Problem set

For each of the following functions, identify the intervals where the function increases, the intervals where the function decreases, the local extreme values and the absolute extreme values.

$\frac{9x+6}{3x^2+7}$
$\frac{x-1}{x^2-x+16}$
$x\sqrt{18-x^2}$
$2x^2\sqrt{10-x}$
$\sqrt[3]{x}(x^2-28)$
$\sqrt[3]{x^2}(x+10)$

Problem set

For each of the following functions, identify the intervals where the function increases, the intervals where the function decreases, the local extreme values and the absolute extreme values.

$(4x^2-5)e^x$
$(18-3x-2x^2)e^x$
$e^x+e^{-x}$
$e^x+3e^{-x} -2x$
$2e^x-6e^{-x} -13x$
$9^x-3^x$
$\frac{1}{e^x+e^{-x}}$

Problem set

For each of the following functions, identify the intervals where the function increases, the intervals where the function decreases, the local extreme values and the absolute extreme values.

$x\ln x$
$x^2\ln 2x$
$\frac{x^2}{4}(5-2\ln 2x)$
$5\ln x+8x-2x^2$
$x^x$ , for $x>0$
$x^{1/x}$ , for $x>0$

Problem set

Find the local and absolute extreme values of the following functions.

$x^3$ in $[-1,1]$
$-x^{1/3}$ in $[-8, 8]$
$x^{1/3}+\cos x$ in $[-6, 6]$
$2x-x\ln x$ in $[1, 10]$
$\begin{cases} x + 1 & \mbox{ if }x \le 1 \\ (x-1)^2+2 & \mbox{ if }x > 1\end{cases}$
$\frac{x^3}{e^x}$

Problem set

Find the local and absolute extreme values of the following functions.

$|2x+1|$
$|3x-5|-4$
$|x^2-4|$
$|16-x^2|-2$
$|\sin x|$
$|\sin x + \cos x|$

Problem set

If $a = 3b-7$ , find the minimum value taken by $ab$ .
Find the two real numbers, that have a difference of $100$ between them, making the smallest product.
Find the dimensions of the rectangle with perimeter $100$ units that has the biggest area.
Find the dimensions of a right triangle with hypotenuse $8$ units that has the biggest area.
Find the biggest area possible for a right triangle that has a hypotenuse of $10$ units.
A right triangle has an area of $50$ square units. What is the smallest possible length of the hypotenuse?
Justify that of all the rectangles that you can form with a certain perimeter, a square has the largest area.
Justify that of all the right-triangles that you can form with a certain hypotenuse, the isosceles right triangle has the largest area.
A farmer bought a fence of length $400'\,$ . He wants to create a fenced rectangular area. What is the maximum area that he can form using the fence that he bought?
A farmer wants to created a fenced rectangular area of $100$ square feet. Determiner the dimensions of the rectangular area so that he needs to buy least length of the fence.

Concavity and graph sketching

Problem set

For each of the following functions, graph the function by determining the intercepts (if possible), horizontal asymptotes, vertical asymptotes, minimums, maximums, concavity and points of inflection.

$y=x^4-8x^3+5$
$y=2x^3-5x^2+4x+11$
$y=2x(x-4)^3$
$y=x(x-5)^4$

Problem set

$y=\frac{4}{x^2-4}$
$y=\frac{8}{x^2+4}$
$y=\frac{x}{x^2+1}$
$y=\frac{3x}{x^2+9}$

Problem set

$y=4x\sqrt{16-x^2}$
$y=\sqrt{9-x^2}$
$y=\frac{1}{\sqrt{x^2+1}}$
$y=\frac{5x}{\sqrt{x^2+25}}$

Problem set

$y=\frac{x^3}{e^x}$
$e^{\sin x}$ in $[0,2\pi]$
$\left(\ln x\right)^2$

Problem set

$y=|x^2-4|$
$y=|2x^2-5x|$

Problem set

In each of the following, the expression for $f'(x)$ is given. For each of the following, determine the minimum/maximum, concavity and points of inflection for the corresponding $f(x)$ , and draw a possible graph of $f(x)$ .

$f'(x) = 3x^2-4x+1$
$f'(x) = 6+5x-x^2$
$f'(x) = 2x^3-16x^2$
$f'(x) = 9x^2-3x^3$

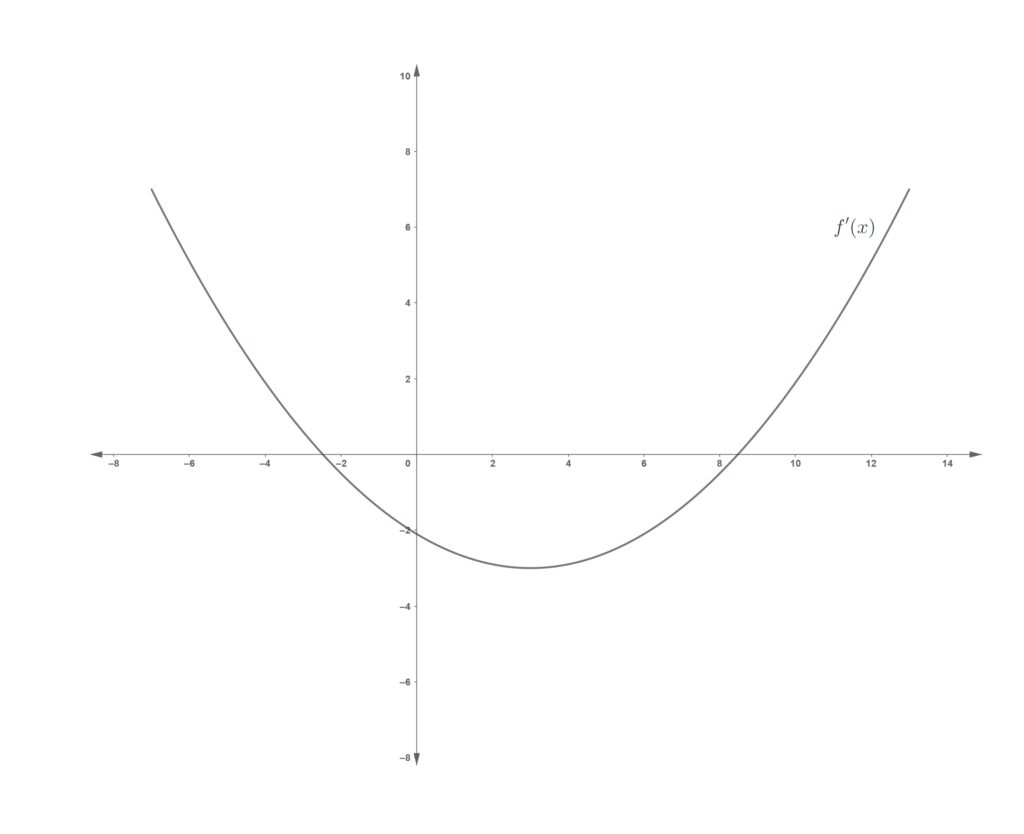
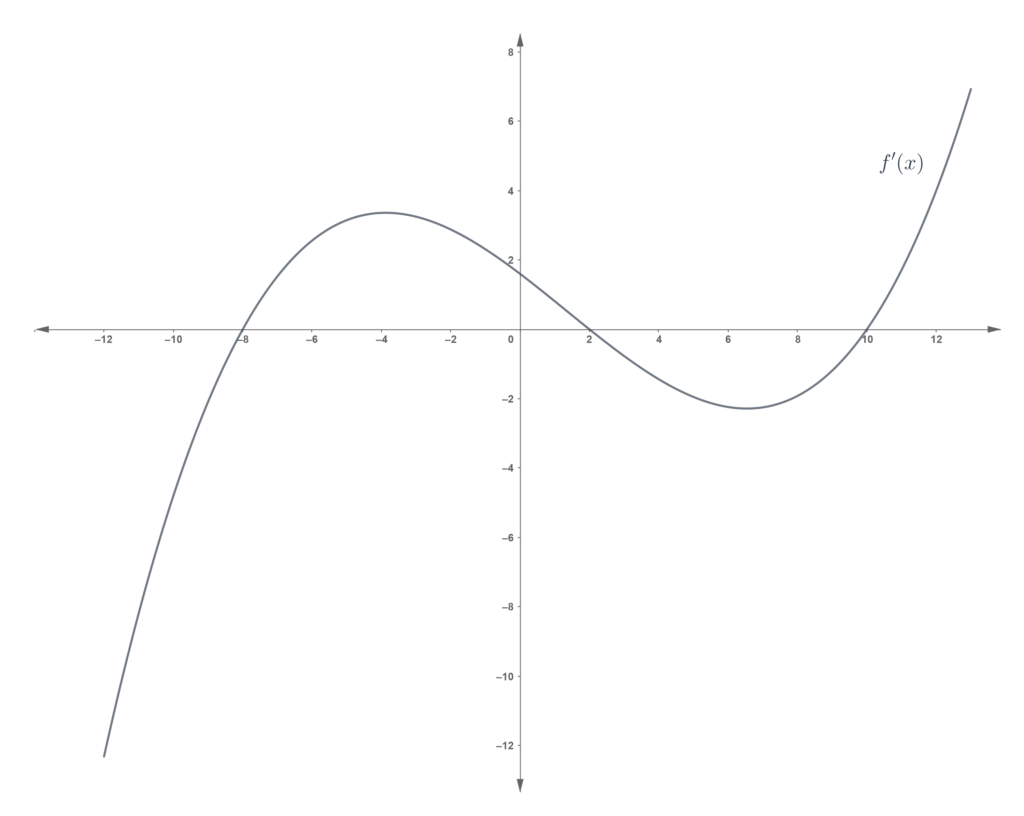
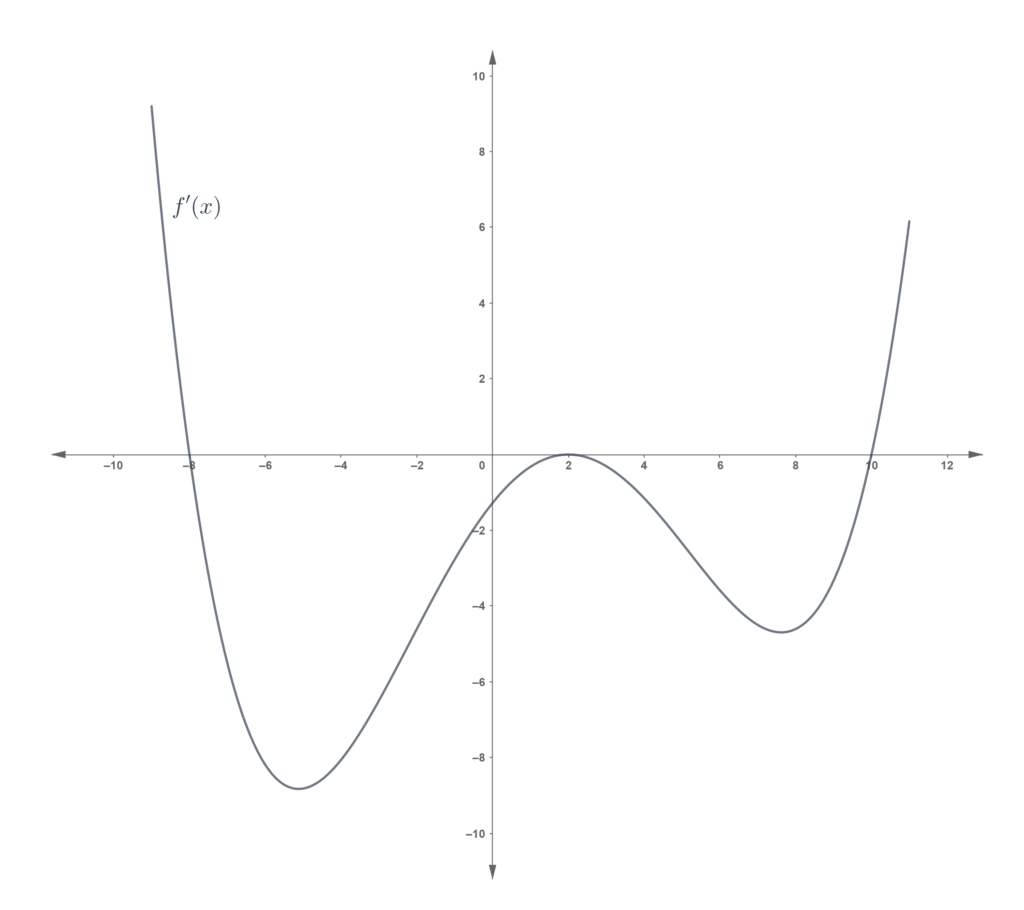
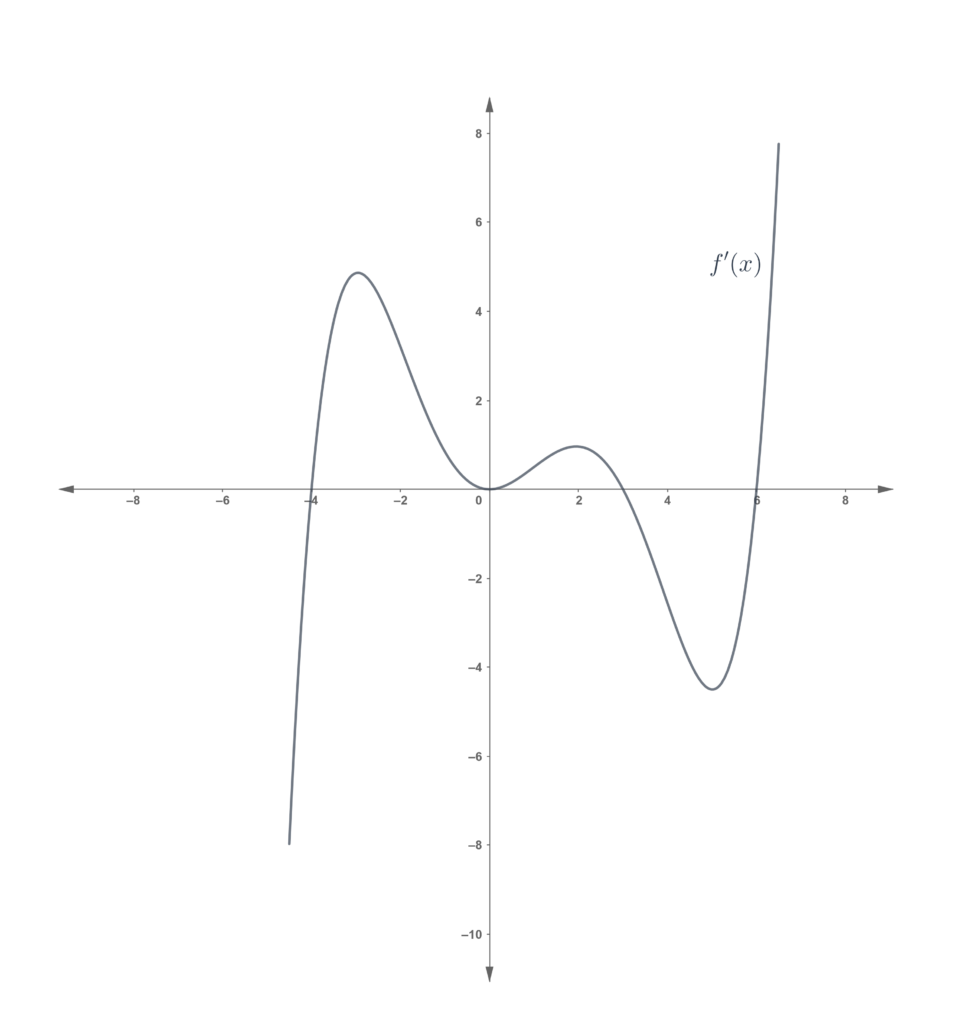
Problem set

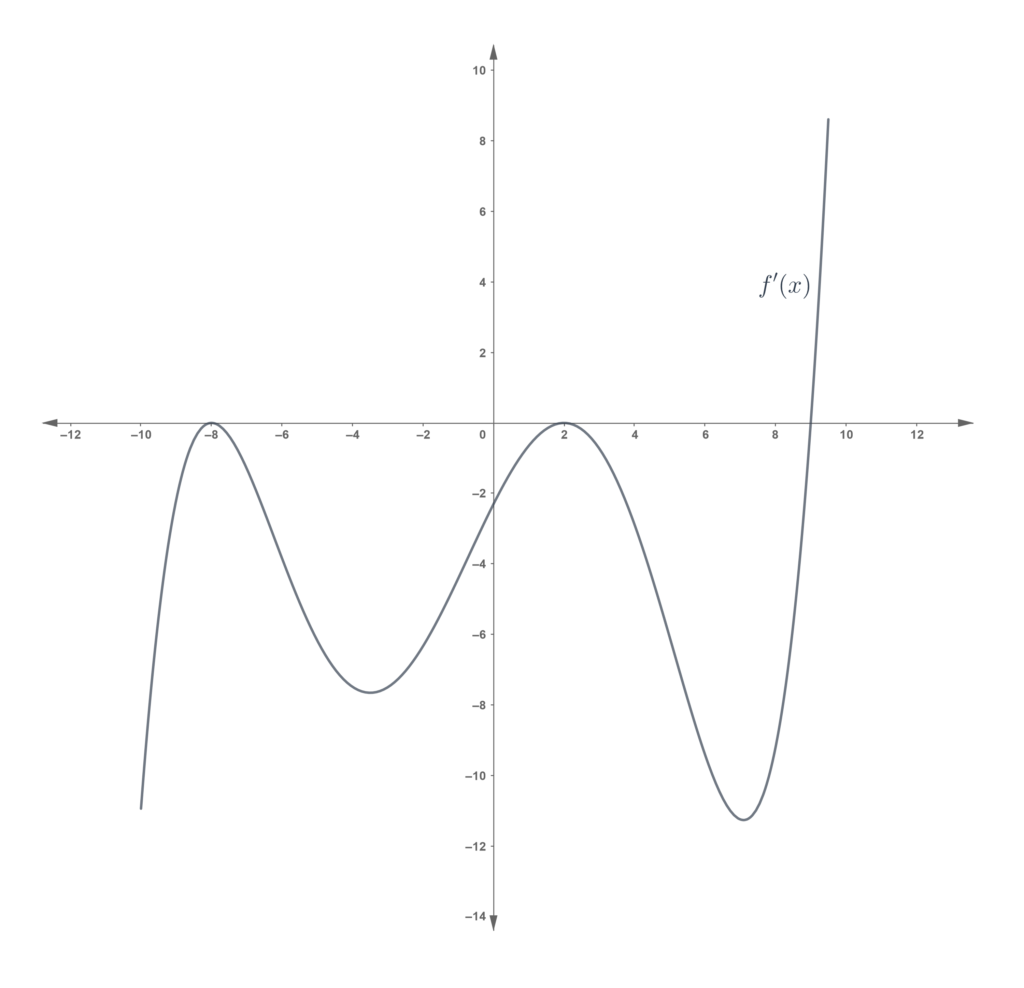
In each of the following, the graph of $f'(x)$ is shown. For each of the following, determine the minimum/maximum, concavity and points of inflection for the corresponding $f(x)$ , and draw a possible graph of $f(x)$ .

What can you infer from derivatives?

Problem set

In the following, assume $f$ is a twice differentiable function – that is, $f''(x)$ exists everywhere in the domain of $f$ . Identify with justification whether each of the following statements is true or false.

$f''(2) > 0$ . This implies $f$ is increasing at $2$ .
$f''(x) < 0$ for all $x$ . It is possible for $f$ to have a local minimum.
$f'(-5) = 0$ and $f'(x) > 0$ for $x > -5$ . This implies $f$ has a minimum at $-5$ .
$f'(x) = (x-1)(9-x)$ . $f$ has a maximum at $x = 9$ .
$f''(-1) < 0$ . This implies $f$ is decreasing at $-1$ .

Problem set

$f'(x)$ has a minimum at $10.1$ . This implies $f$ has a point of inflection at $10.1$
$f'(3.2) = 0$ . This implies $f$ has an extremum at $3.2$ .
$f''(-10) = 0$ . This implies $f$ has a point of inflection at $-10$ .
$f'(-2.9) = 0$ , and $f''(-2.9) < 0$ . This implies $f$ has a point of inflection at $-2.9$
$f'(4) = 0$ . This implies $f$ has a point of inflection at $4$ .

Problem set

$f'(-5) = 0$ , $f'(x) > 0$ for $x > -5$ and $f'(x) < 0$ for $x < -5$ . This implies $f$ has a minimum at $-5$ .
$f'(x) = (x-1)(9-x)^2$ . $f$ has a maximum at $x = 9$ .
$f''(x) < 0$ for all $x$ . It is possible for $f$ to have a local maximum.
$f''(4) = 0$ . This implies $f$ has an extremum at $4$ .
$f'(x)$ has a maximum at $10.1$ . This implies $f$ has a point of inflection at $10.1$

Problem set

$f'(x)$ has a minimum at $10.1$ . This implies $f$ concaves up to the immediate right of $10.1$
$f'(-3.1) = 0$ and $f''(-3.1) = 0$ . This implies $f$ has an extremum at $-3.1$ .
$f''(0) = 0$ . This implies $f$ has a point of inflection at $0$ .
$f$ has a point of inflection at $3$ . This implies $f''(3) = 0$ .
$f$ has a point of inflection at $3$ . This implies $f$ has an extremum at $3$ .

Real-world applications

Problem set

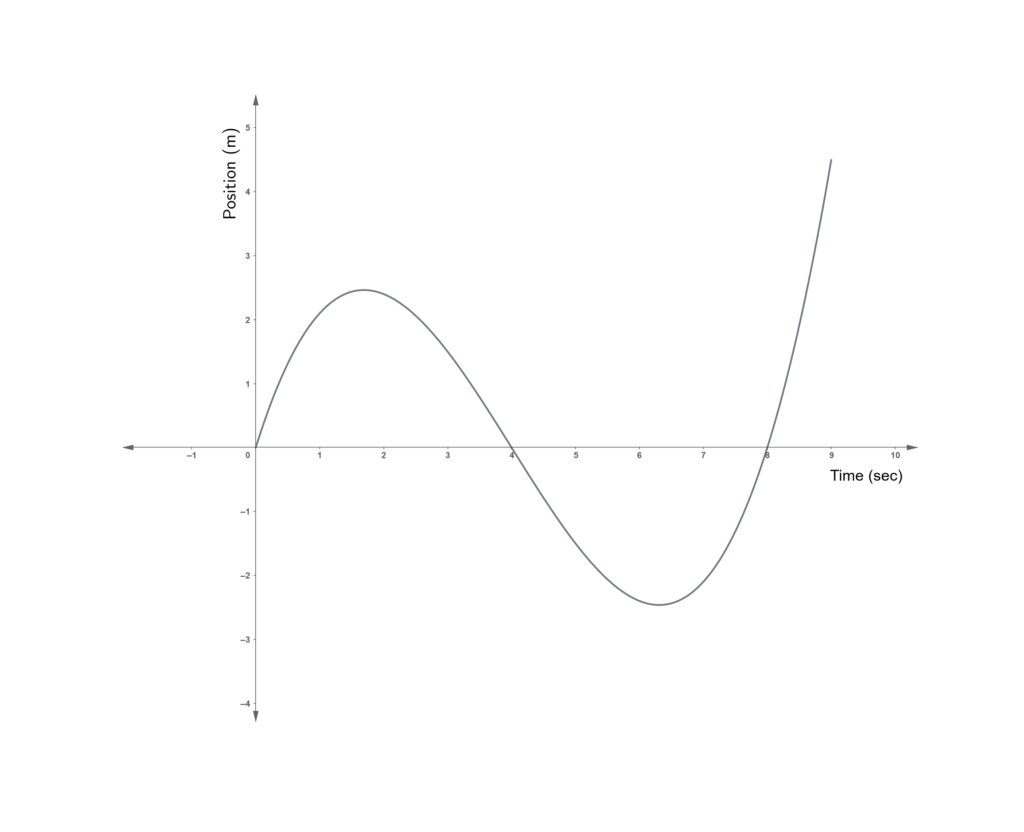
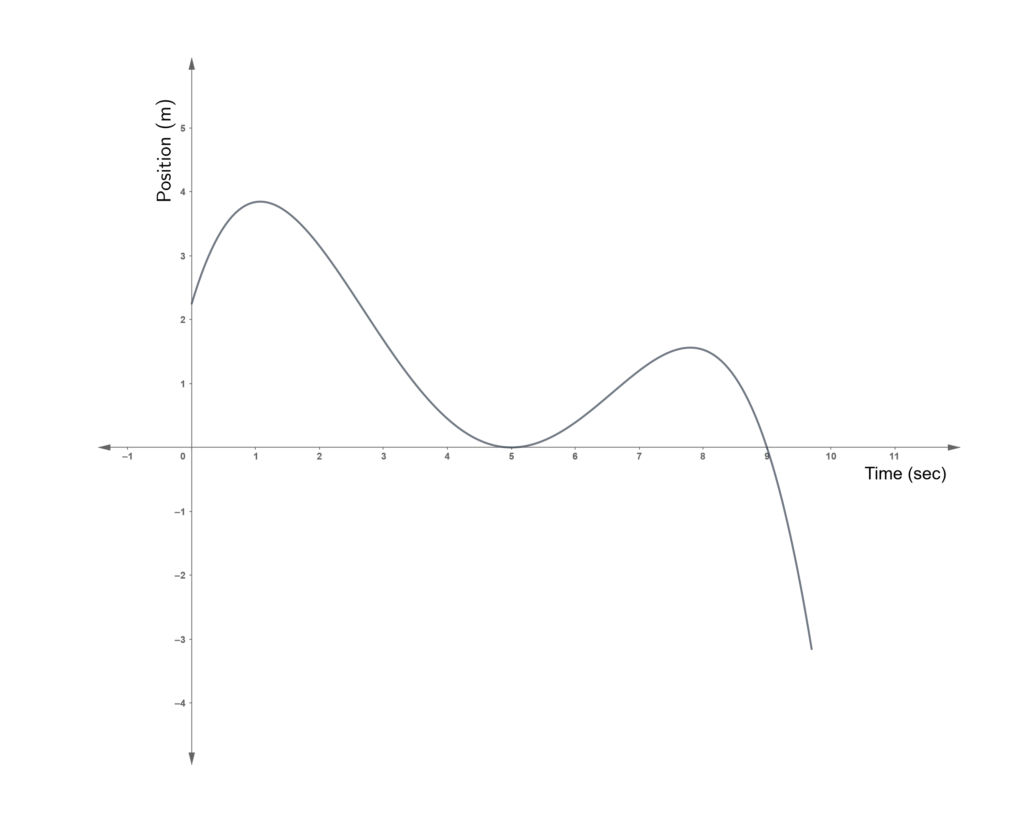
In each of the following problems, the position of a particle moving along the X-axis is given as a function of time. For each of the problems, describe the motion of the particle by doing the following:

identify the time instant when the particle changed direction
the maximum distance the particle would be from the origin
the time intervals when the particle is moving away from the origin and moving towards the origin
the time-intervals when the particle is accelerating or decelerating

$x(t) = t^3 +2t^2 -4t-10$
$x(t) = 4t^3 - 4t^2 + t - 2$
$x(t) = 4t^3 - 5t^2 + 2t - 5$
$x(t) = 5t^4 - t^3 - t^2 + 2$

Problem set

Use tables giving the behavior of a function such as horizontal tangent, concavity, rising, falling etc to draw the graph of a function.
Use tables giving values of derivative and the second derivative to sketch the graph of a function.