Learn – Calculus – Definite Integrals

Summations

Sigma notation

Exercises

Problem set

Express each of the following using sigma notation.

$1 + 2 + 3 + \cdots + 1000$
$1^3 + 2^3 + 3^3 + \cdots + 719^3$
$2\times 1^2 + 2\times 2^2 + 2\times 3^2 + \cdots + 2\times 500^2 + 2\times 501^2$
$3\times \sqrt{5} + 3\times \sqrt{6} + 3\times \sqrt{7} + \cdots + 3\times \sqrt{981}$
$10\times \left(\frac{1}{2}\right)^{1} + 10\times \left(\frac{1}{2}\right)^{2} + 10\times \left(\frac{1}{2}\right)^{3} + \cdots + 10\times \left(\frac{1}{2}\right)^{n}$

Problem set

Express each of the following using sigma notation.

$a_1 + a_2 + a_3 + \cdots + a_{679}$
$b_5 + b_6 + b_7 + \cdots + b_{n}$
$1\times c_1 + 2\times c_2 + 3\times c_3 + \cdots + 501\times c_{501}$
$2\times\frac{c_1}{1} + 2\times \frac{c_2}{2} + 2\times \frac{c_3}{3} + \cdots + 2\times \frac{c_{n}}{n}$
$\frac{c_1^2}{2} + \frac{c_2^2}{2} + \frac{c_3^2}{2} + \cdots + \frac{c_{n}^2}{2}$
$0.5\times f\left(c_1\right) + 0.5\times f\left(c_2\right) + 0.5\times f\left(c_3\right) + \cdots + 0.5\times f\left(c_n\right)$
$g\left(c_1\right)\times 0.2+ g\left(c_2\right)\times 0.2+ g\left(c_3\right)\times 0.2+ \cdots + g\left(c_n\right)\times 0.2$

Problem set

Give the hundredth term in each of the following.

$\sum\limits_{k=1}^{501} \frac{k^2}{5}$
$\sum\limits_{k=1}^{n} \frac{101\sqrt{k}}{k+1}$
$\sum\limits_{k=1}^{n} 5\times\left(\frac{1}{5}\right)^k$
$\sum\limits_{k=1}^{n} 0.2\times c_k^2$
$\sum\limits_{k=1}^{n} 0.5f\left(c_k\right)$

Riemann Sums

Exercises

Problem set

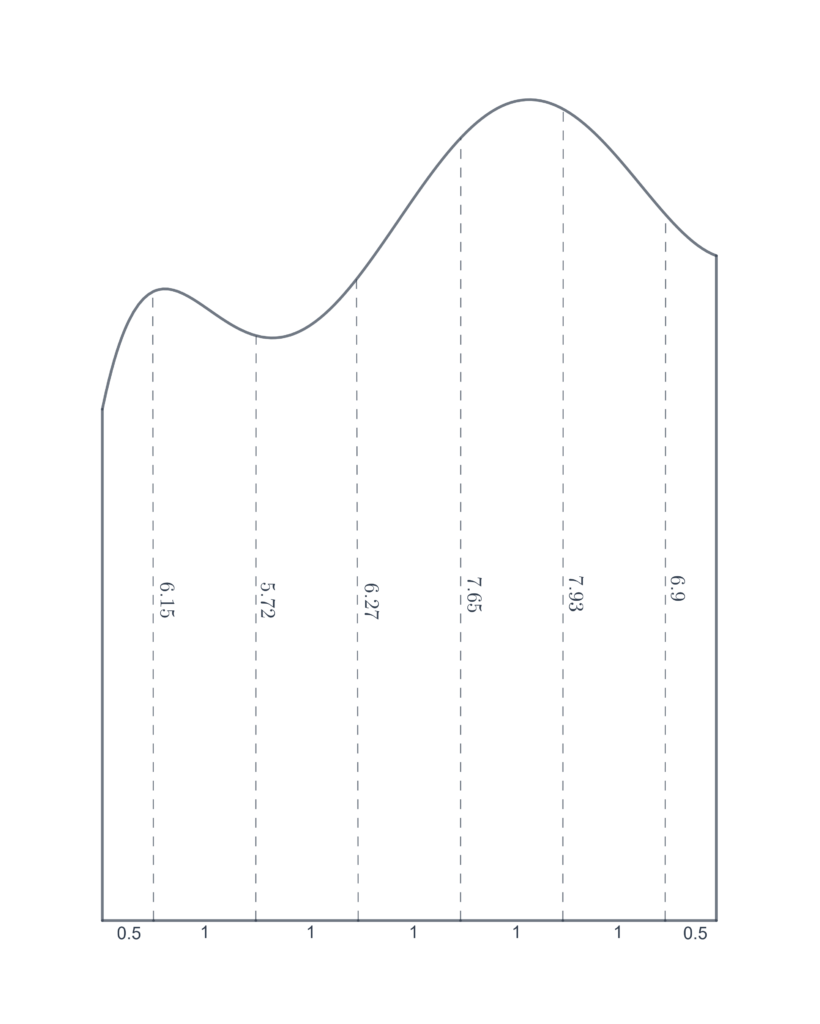
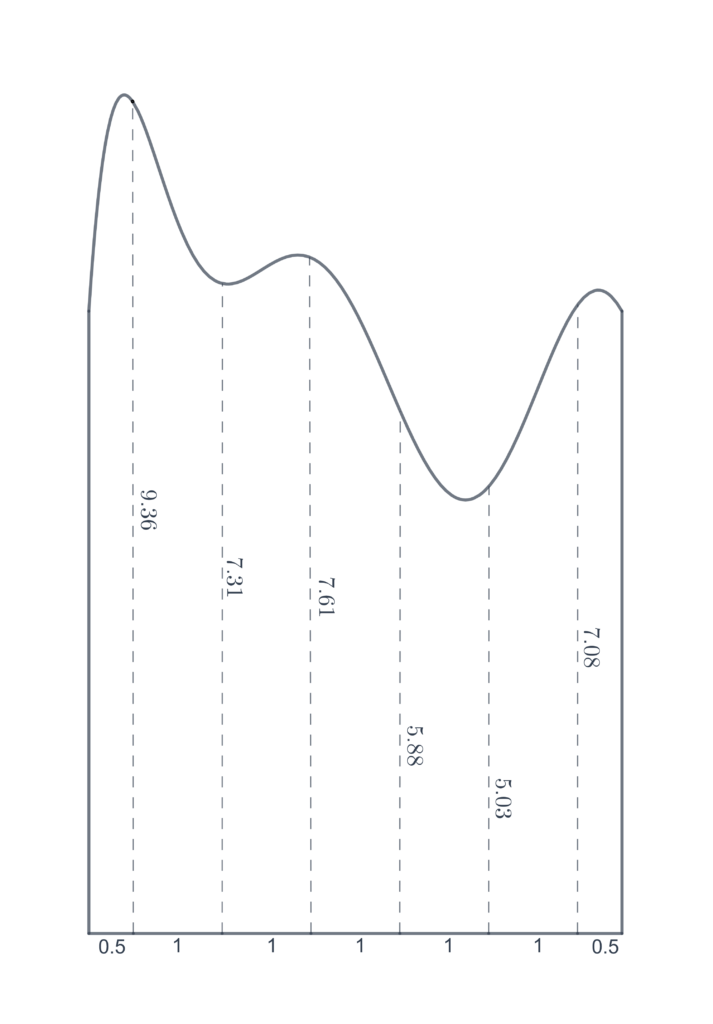
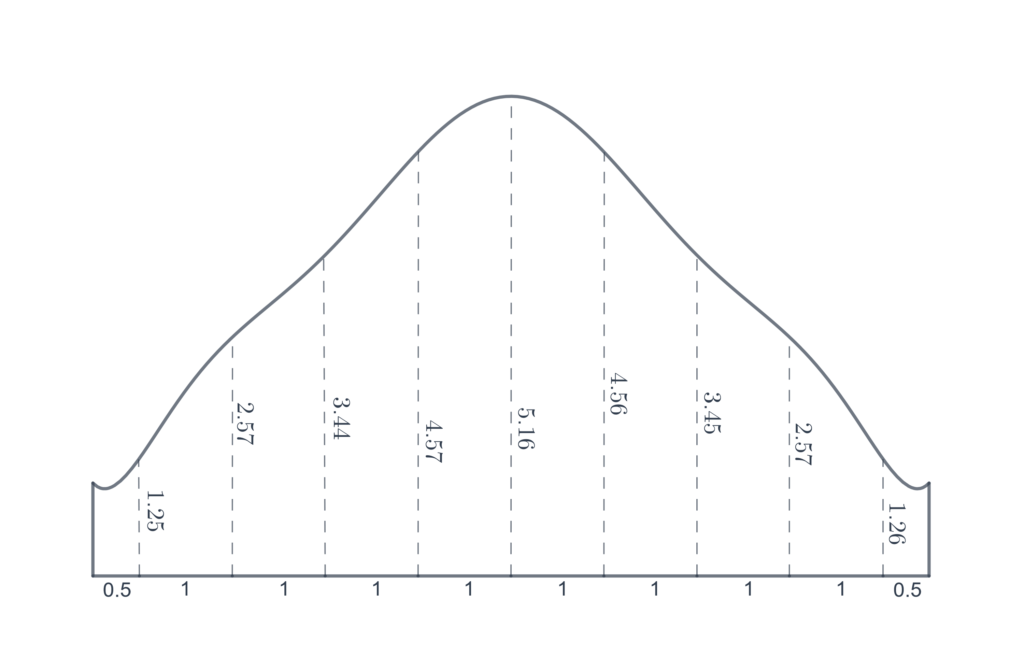
For each of the following problems, approximately calculate the area of the figure, by dividing it up into rectangles. Assume the lengths of line segments as shown.

Problem set

The following table gives values for a non-negative continuous function. Approximate the area between the function’s curve and the X-axis from $x = 1$ through $x = 8$ .

$\boldsymbol{x}$ $\boldsymbol{f(x)}$

$1.5$ $5$

$2.5$ $3$

$3.5$ $2$

$4.5$ $2.5$

$5.5$ $4$

$6.5$ $6$

$7.5$ $9$

The following table gives values for a non-negative continuous function. Approximate the area between the function’s curve and the X-axis from $x = 3$ through $x = 7$ .

$\boldsymbol{x}$ $\boldsymbol{f(x)}$

$3.25$ $2$

$3.75$ $5$

$4.25$ $7$

$4.75$ $3$

$5.25$ $1$

$5.75$ $4$

$6.25$ $6$

$6.75$ $5$

The following table gives values for a non-negative continuous function. Approximate the area between the function’s curve and the X-axis from $x = 2$ through $x = 4$ .

$\boldsymbol{x}$ $\boldsymbol{f(x)}$

$2.1$ $5$

$2.3$ $15$

$2.5$ $10$

$2.7$ $5$

$2.9$ $7.5$

$3.1$ $5$

$3.3$ $2.5$

$3.5$ $7.5$

$3.7$ $10$

$3.9$ $12.5$

Give an approximation of the area between the curve $\ln x$ and the X-axis over the interval $[3,7]$ , by dividing the interval is $8$ sub-intervals.
Give an approximation of the area between the curve $\sqrt{x}$ and the X-axis over the interval $[1,6]$ , by dividing the interval is $10$ sub-intervals.
Find the approximate area under the $\sin x$ curve over $[0,\pi]$ , by dividing the interval is $4$ sub-intervals.
Give an approximation of the area between the curves $x^2$ and $\frac{1}{x}$ over the interval $[10,15]$ , by dividing the interval into $10$ sub-intervals.
Give an approximation of the area between the curves $\sin x$ and $\cos x$ over the interval $\left[0,\frac{\pi}{4}\right]$ , by dividing the interval into $4$ sub-intervals.
Give an approximation of the area between the curves $\sqrt{x}$ and $\frac{1}{x^2}$ over the interval $[2,6]$ , by dividing the interval into $8$ sub-intervals.

$\boldsymbol{x}$	$\boldsymbol{f(x)}$
$1.5$	$5$
$2.5$	$3$
$3.5$	$2$
$4.5$	$2.5$
$5.5$	$4$
$6.5$	$6$
$7.5$	$9$

$\boldsymbol{x}$	$\boldsymbol{f(x)}$
$3.25$	$2$
$3.75$	$5$
$4.25$	$7$
$4.75$	$3$
$5.25$	$1$
$5.75$	$4$
$6.25$	$6$
$6.75$	$5$

$\boldsymbol{x}$	$\boldsymbol{f(x)}$
$2.1$	$5$
$2.3$	$15$
$2.5$	$10$
$2.7$	$5$
$2.9$	$7.5$
$3.1$	$5$
$3.3$	$2.5$
$3.5$	$7.5$
$3.7$	$10$
$3.9$	$12.5$

Problem set

A flower vase is of height $7$ inches. It has different cross-sectional areas at different heights from its base. The cross-sectional areas are shown in the table below.

Height from base (in inches) Cross-sectional area (in square inches)

$0$ $3$

$0.5$ $4$

$1.5$ $5$

$2.5$ $3$

$3.5$ $5$

$4.5$ $4$

$5.5$ $4$

$6.5$ $3.5$

$7.0$ $3$

Approximately calculate the volume of the inside of the flower vase.

A flower vase is of height $4$ inches. It has different cross-sectional areas at different heights from its base. The cross-sectional areas are shown in the table below.

Height from base (in inches) Cross-sectional area (in square inches)

$0$ $3$

$0.25$ $4$

$0.75$ $5$

$1.25$ $3$

$1.75$ $5$

$2.25$ $4$

$2.75$ $4$

$3.25$ $3.5$

$3.75$ $3$

$4$ $2.8$

Approximately calculate the volume of the inside of the flower vase.

A concrete mixer is of height $10$ feet. It has has circular cross-sections with different radii at different heights from the base. The cross-sectional radii are shown in the table below.

Height from base (in feet) Radius of cross-section (in feet)

$0$ $2$

$0.5$ $2.5$

$1.5$ $3.0$

$2.5$ $3.5$

$3.5$ $3.7$

$4.5$ $3.7$

$5.5$ $3.5$

$6.5$ $3.0$

$7.5$ $3.2$

$8.5$ $3.5$

$9.5$ $3.2$

$10.0$ $3.0$

Approximately calculate the volume of the inside of the mixer.

The following table gives the speedometer readings of speed of a car at various points of time.

Time (in minutes) Speed (in mph)

$0$ $0$

$0.5$ $15$

$1.5$ $30$

$2.5$ $50$

$3.5$ $55$

$4.5$ $60$

$5.5$ $55$

$6.5$ $45$

$7.5$ $20$

$8.5$ $40$

$9.5$ $50$

Approximately calculate the distance traveled by the car in $10$ minutes.

The following table gives the speedmeter readings of speed of a plane at various points of time.

Time (in minutes) Speed (in mph)

$0$ $0$

$0.25$ $20$

$0.75$ $40$

$1.25$ $70$

$1.75$ $110$

$2.25$ $160$

$2.75$ $220$

$3.25$ $280$

$3.75$ $330$

$4.25$ $300$

$4.75$ $310$

Approximately calculate the distance traveled by the plane in $5$ minutes.

A water tank had $20$ cubic feet of water. At time $t = 5$ seconds, water was let into the tank. The rates of flow of water at different times are shown in the table.

Time (in seconds) Rate of flow (in Cubic feet/sec)

$6$ $2$

$8$ $3$

$10$ $4$

$12$ $3$

$14$ $5$

$16$ $2$

$18$ $3$

$20$ $1$

Approximately calculate how much water would be in the tank at $t=21$ seconds.

Oil is being pumped out into a tanker from an oil well. When checked at $10$ AM, the tanker already had $27$ gallons of oil. The following table shows the rates of pumping oil out at various points of time.

Time Rate of pumping out (in gallons/sec)

$10:05$ AM $3$

$10:15$ AM $5$

$10:30$ AM $7$

$10:38$ AM $4$

$10:50$ AM $5$

$10:57$ AM $2$

Approximately calculate how much oil would be in the tank at $11$ AM.

$10$ feet of a heavy iron chain is dangling from the roof of a building along a wall of the building. If the iron chain weighs $2$ lb/foot, approximately calculate the work in foot-pounds that needs to done in order to pull the entire chain onto the roof. From physics, the work done in pulling an object of weight $w$ lb up a distance of $d$ feet is given by $wd$ foot-pounds.

Height from base (in inches)	Cross-sectional area (in square inches)
$0$	$3$
$0.5$	$4$
$1.5$	$5$
$2.5$	$3$
$3.5$	$5$
$4.5$	$4$
$5.5$	$4$
$6.5$	$3.5$
$7.0$	$3$

Height from base (in inches)	Cross-sectional area (in square inches)
$0$	$3$
$0.25$	$4$
$0.75$	$5$
$1.25$	$3$
$1.75$	$5$
$2.25$	$4$
$2.75$	$4$
$3.25$	$3.5$
$3.75$	$3$
$4$	$2.8$

Height from base (in feet)	Radius of cross-section (in feet)
$0$	$2$
$0.5$	$2.5$
$1.5$	$3.0$
$2.5$	$3.5$
$3.5$	$3.7$
$4.5$	$3.7$
$5.5$	$3.5$
$6.5$	$3.0$
$7.5$	$3.2$
$8.5$	$3.5$
$9.5$	$3.2$
$10.0$	$3.0$

Time (in minutes)	Speed (in mph)
$0$	$0$
$0.5$	$15$
$1.5$	$30$
$2.5$	$50$
$3.5$	$55$
$4.5$	$60$
$5.5$	$55$
$6.5$	$45$
$7.5$	$20$
$8.5$	$40$
$9.5$	$50$

Time (in minutes)	Speed (in mph)
$0$	$0$
$0.25$	$20$
$0.75$	$40$
$1.25$	$70$
$1.75$	$110$
$2.25$	$160$
$2.75$	$220$
$3.25$	$280$
$3.75$	$330$
$4.25$	$300$
$4.75$	$310$

Time (in seconds)	Rate of flow (in Cubic feet/sec)
$6$	$2$
$8$	$3$
$10$	$4$
$12$	$3$
$14$	$5$
$16$	$2$
$18$	$3$
$20$	$1$

Time	Rate of pumping out (in gallons/sec)
$10:05$ AM	$3$
$10:15$ AM	$5$
$10:30$ AM	$7$
$10:38$ AM	$4$
$10:50$ AM	$5$
$10:57$ AM	$2$

Problem set

The velocity of a plane from the start to the liftoff at $30$ seconds is given by the function $v(t) = t^2-26t+20$ . Approximately calculate the distance traveled by the aircraft during the takeoff using a sum of $10$ terms.
A water tank is of height $4$ feet. The cross-sectional area of the tank at height $h$ feet from its base is given by the function $a(h) = \frac{\pi h^2}{16}$ square feet. Express the volume of the water tank using a sum of $8$ terms.
A freight container of height $5$ feet has circular cross-sectional areas. If the radius of the cross-section at height $h$ from the base is given by $\sqrt{25-h^2}$ , express the volume of the container as a sum of $10$ terms.
The sum $0.5\times 0.25^2+0.5\times 0.75^2+0.5\times 1.25^2+0.5\times 1.75^2+0.5\times 2.25^2+0.5\times 2.75^2$ approximates the area under a certain curve over a certain interval. Identify the curve and interval.

Definition and notation

Exercises

Problem set

Using the geometric interpretation of $\int\limits_a^b f(x)\,dx$ as the area under the curve $f(x)$ , evaluate the following.

$\int\limits_0^4 x\, dx$

$\int\limits_1^5 x\, dx$

$\int\limits_2^6 2x\, dx$

$\int\limits_0^8 -x\, dx$

$\int\limits_{-6}^{-2}\frac{x}{2}\, dx$

$\int\limits_{-2}^3 2x\, dx$

Problem set

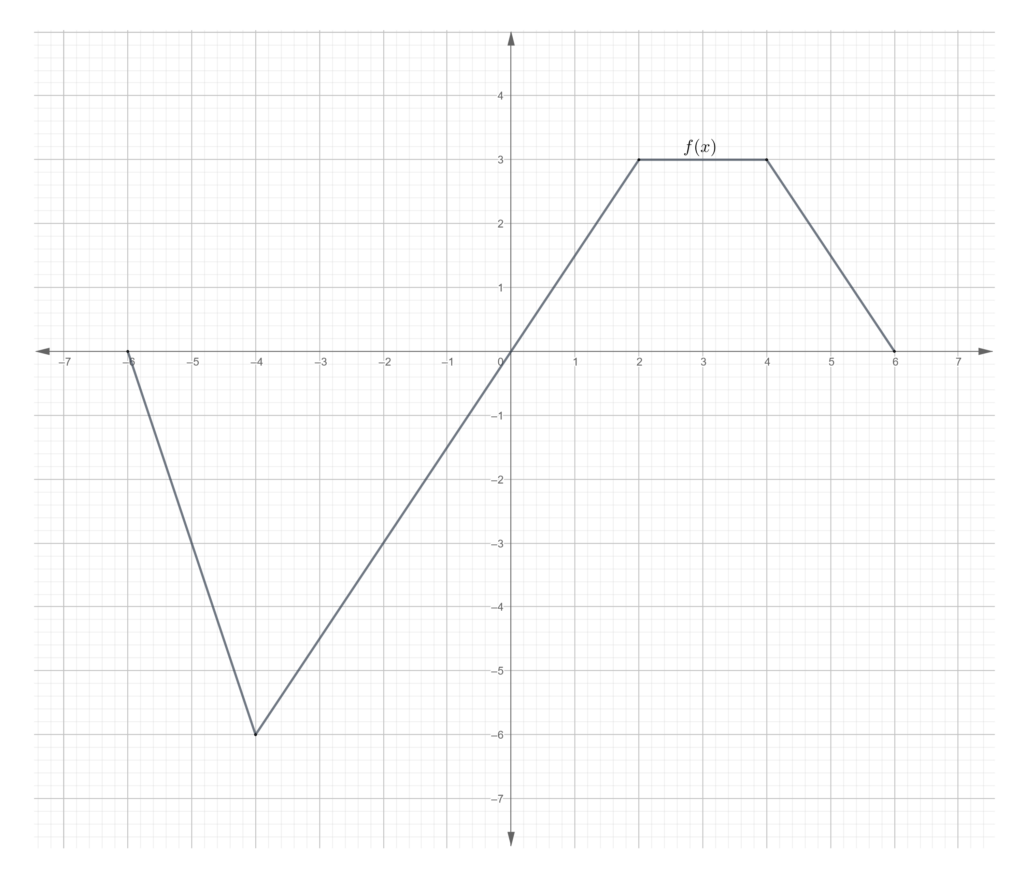
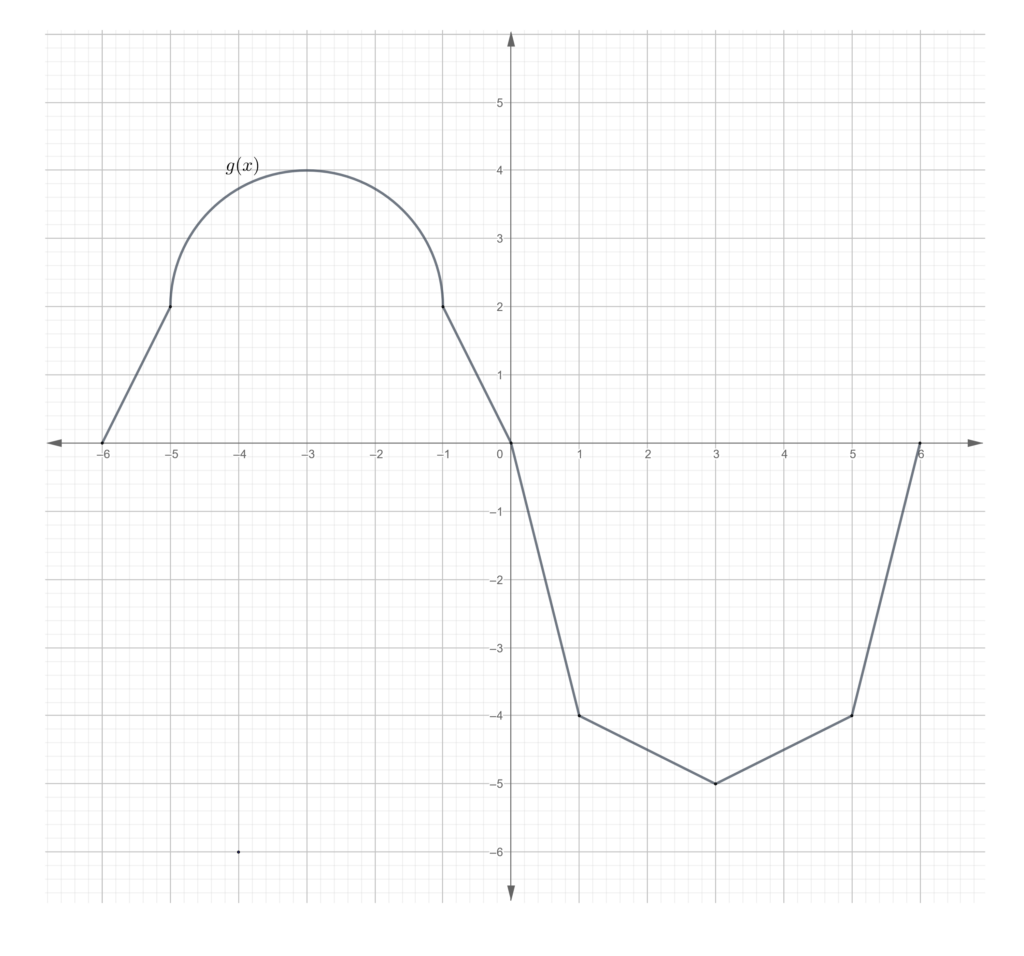
In each of the following problems, evaluate the integral based on the graph of the function.

$\int\limits_{-6}^6 f(x)\, dx$

$\int\limits_{-6}^6 g(x)\, dx$

Problem set

Consider an interval $[a, b]$ . Let the interval be divided into $n$ sub-intervals each of width $\Delta x$ . Let $c_k$ be a point in the $k$ th sub-interval. Express each of the following in the notation of the definite integral.

$\lim\limits_{\Delta x\to 0}\sum\limits_{k=1}^{n}c_k^3\,\Delta x$

$\lim\limits_{\Delta x\to 0}\sum\limits_{k=1}^{n}\frac{\log c_k}{c_k+1}\,\Delta x$

$\lim\limits_{\Delta x\to 0}\sum\limits_{k=1}^{n}(\sin 2c_k+ \cos c_k +5)\,\Delta x$

$\lim\limits_{\Delta x\to 0}\sum\limits_{k=1}^{n}e^{\frac{-c_k^2}{2}}\,\Delta x$

$\lim\limits_{\Delta x\to 0}\sum\limits_{k=1}^{n}\frac{c_k}{\sqrt{c_k^2+1}}\,\Delta x$

Properties

Exercises

Problem set

Assume an integrable function $f(x)$ .

If $\int\limits_1^2 f(x)\,dx = 5$ , what can you say about $\int\limits_2^2 f(x)\,dx$ ?

If $\int\limits_1^2 f(x)\,dx = 5$ , what can you say about $\int\limits_2^1 f(x)\,dx$ ?

If $\int\limits_{-1}^{1} f(x)\,dx = 10$ , what can you say about $\int\limits_{1}^{-1} f(x)\,dx$ ?

If $\int\limits_1^2 f(x)\,dx = 5$ , what can you say about $\int\limits_{-1}^{-2} f(x)\,dx$ ?

If $\int\limits_{-1}^{1} f(x)\,dx = 10$ , what can you say about $\int\limits_{0}^{1} f(x)\,dx$ ?

If $\int\limits_{0}^{1} f(x)\,dx = 10$ , what can you say about $\int\limits_{0}^{2} f(x)\,dx$ ?

If $\int\limits_0^8 f(x)\,dx = 10$ , what can you say about $\int\limits_{0}^{4} f(x)\,dx$ ?

Problem set

Assume an integrable function $f(x)$ .

If $\int\limits_1^2 f(x)\,dx = 10$ and $\int\limits_2^5 f(x)\,dx = 5$ , what can you say about $\int\limits_{1}^{5} f(x)\,dx$ ?

If $\int\limits_1^5 f(x)\,dx = 10$ and $\int\limits_1^2 f(x)\,dx = 5$ , what can you say about $\int\limits_{2}^{5} f(x)\,dx$ ?

If $\int\limits_1^5 f(x)\,dx = 10$ and $\int\limits_2^5 f(x)\,dx = 5$ , what can you say about $\int\limits_{1}^{2} f(x)\,dx$ ?

If $\int\limits_1^5 f(x)\,dx = 10$ and $\int\limits_1^2 f(x)\,dx = 5$ , what can you say about $\int\limits_{3}^{5} f(x)\,dx$ ?

If $\int\limits_1^5 f(x)\,dx = 10$ and $\int\limits_5^2 f(x)\,dx = 5$ , what can you say about $\int\limits_{1}^{2} f(x)\,dx$ ?

If $\int\limits_{-1}^{-5} f(x)\,dx = 10$ and $\int\limits_{-2}^{-5} f(x)\,dx = 5$ , what can you say about $\int\limits_{-2}^{-1} f(x)\,dx$ ?

Problem set

Assume an integrable function $f(x)$ .

If $\int\limits_1^5 f(x)\,dx = 10$ , what can you say about $\int\limits_{1}^{5} 2f(x)\,dx$ ?

If $\int\limits_1^5 f(x)\,dx = 10$ , what can you say about $\int\limits_{5}^{5} 2f(x)\,dx$ ?

If $\int\limits_1^5 f(x)\,dx = 10$ , what can you say about $\int\limits_{5}^{1} -f(x)\,dx$ ?

If $\int\limits_1^5 f(x)\,dx = 10$ , what can you say about $\int\limits_{-5}^{-1} -2f(x)\,dx$ ?

If $\int\limits_{-1}^{1} f(x)\,dx = 10$ , what can you say about $\int\limits_{0}^{1} 2f(x)\,dx$ ?

Problem set

Assume integrable functions $f(x)$ and $g(x)$ .

If $\int\limits_1^5 f(x)\,dx = 10$ and $\int\limits_1^5 g(x)\,dx = 5$ , what can you say about
$\int\limits_{1}^{5} f(x)+g(x)\,dx$ ?

If $\int\limits_1^5 f(x)\,dx = 10$ and $\int\limits_5^1 g(x)\,dx = 5$ , what can you say about
$\int\limits_{1}^{5} f(x)+g(x)\,dx$ ?

If $\int\limits_1^3 f(x)\,dx = 10$ and $\int\limits_3^5 g(x)\,dx = 5$ , what can you say about
$\int\limits_{1}^{5} f(x)+g(x)\,dx$ ?

If $\int\limits_{-1}^{-5} f(x)\,dx = 10$ and $\int\limits_{-1}^{-5} g(x)\,dx = 5$ , what can you say about
$\int\limits_{-5}^{-1} f(x)-g(x)\,dx$ ?

If $\int\limits_1^5 f(x)\,dx = 10$ and $\int\limits_{-1}^{-5} g(x)\,dx = 5$ , what can you say about
$\int\limits_{1}^{5} f(x)-g(x)\,dx$ ?

Problem set

A straight line has equation $y = mx$ . If $\int\limits_1^3 y\,dx = 10$ , find the value of $m$ .
Straight line on either side of origin
Even and odd function integrals

Average value of a function

Exercises

Problem set

Find the average value of the function $\frac{1}{x}$ in $[1,e]$ .
A car’s speed is given by $s(t) = 50 + 6t^2$ , where $t$ is given in minutes. What is the average speed of the car from the starting time to $10$ minutes.
The average value of a non-negative function in is .
1. What is the area between the graph of the function and the $X$ -axis, measured between $-5$ and $5$ on the $X$ -axis?
2. How would you answer the above the question if the function is not given to be non-negative?