Definition
Exercises
Problem set
Find for each of the following using the definition of the derivative.
Problem set
Find the value of each of the following assuming .
Problem set
Find for each of the following using the definition of the derivative.
Geometric significance and differentiability
Exercises
Problem set
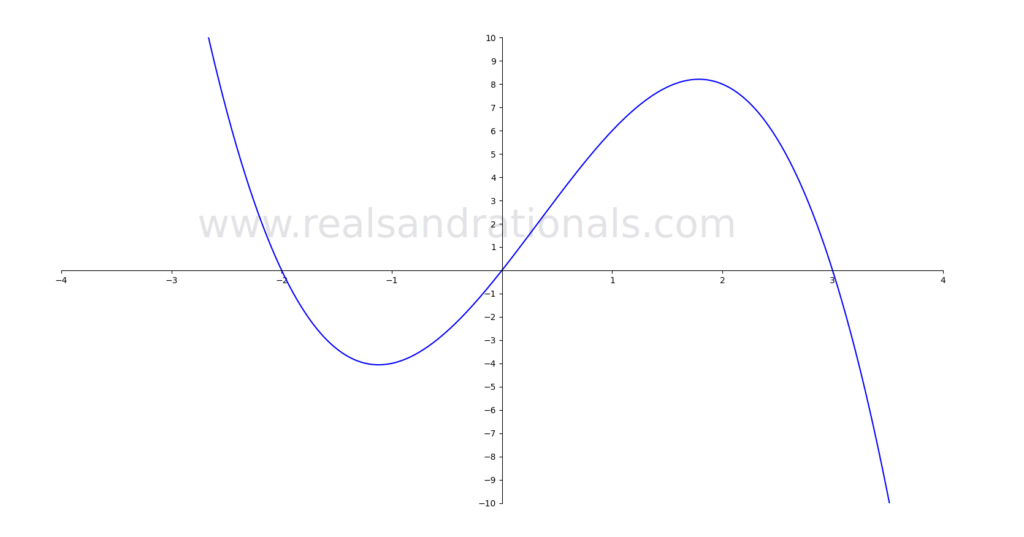
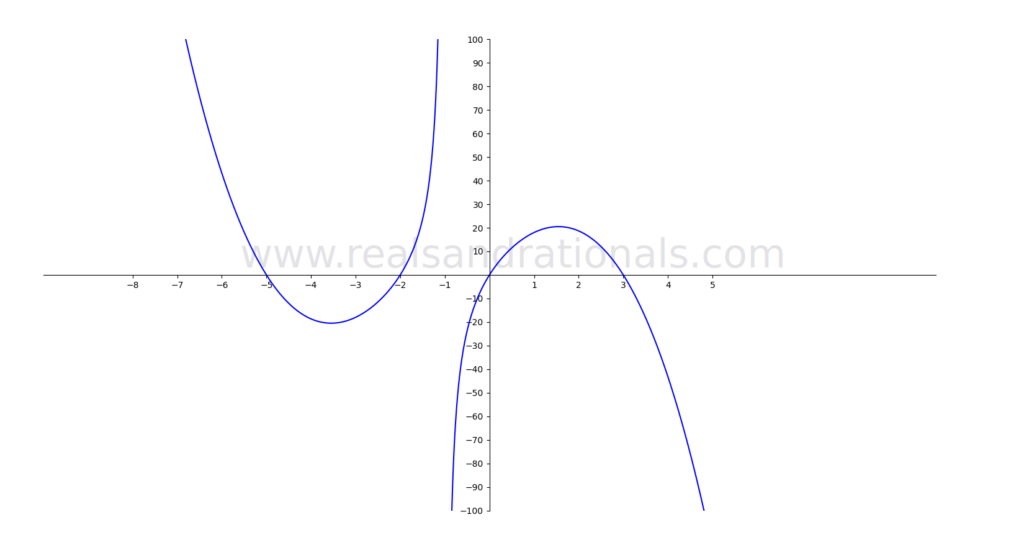
- For the function
shown below, estimate the following:
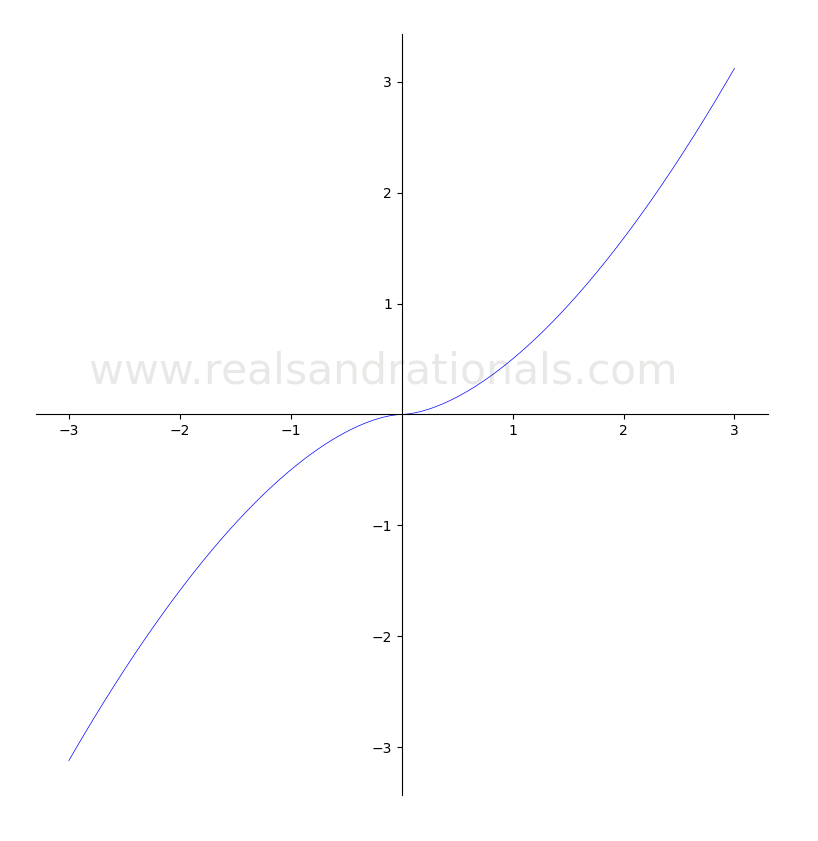
- For the function
shown below, estimate the following:
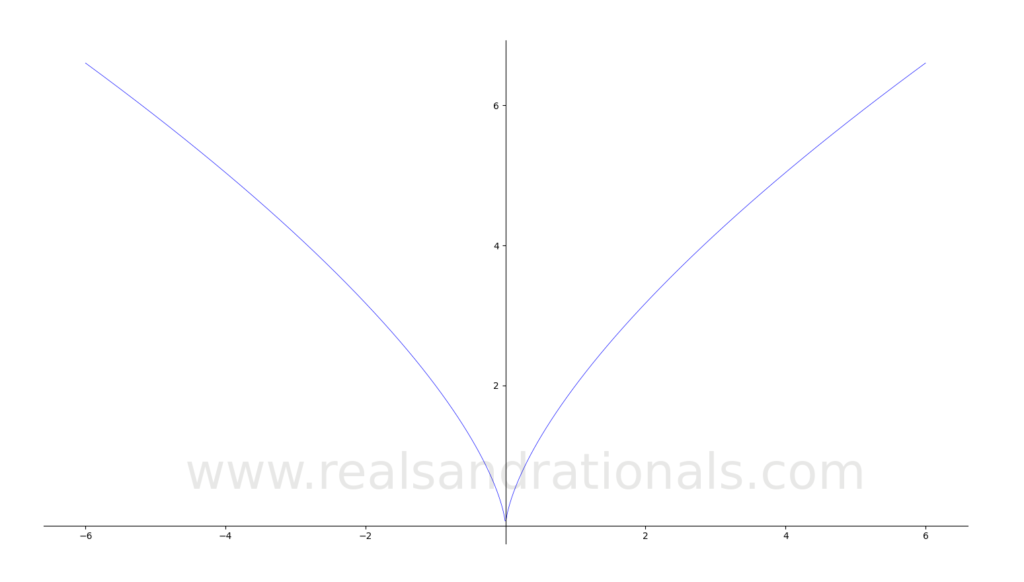
Problem set
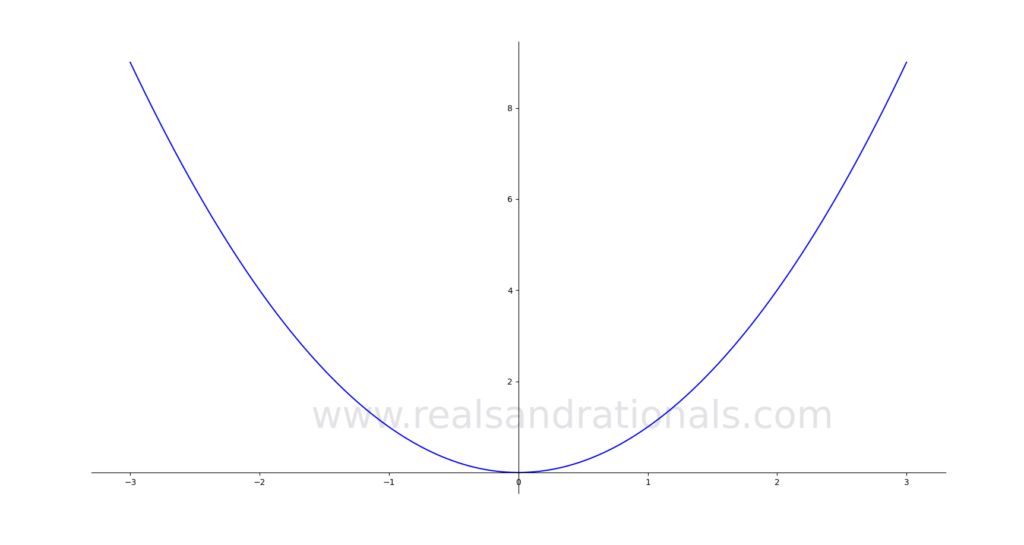
Identify where each of the following functions is differentiable.
Problem set
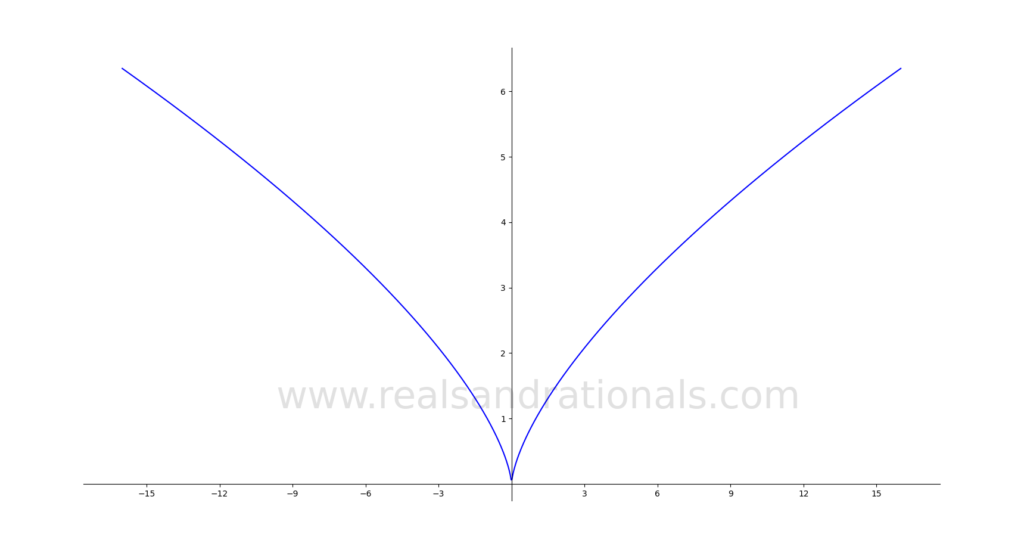
Identify where each of the following functions is differentiable.
Problem set
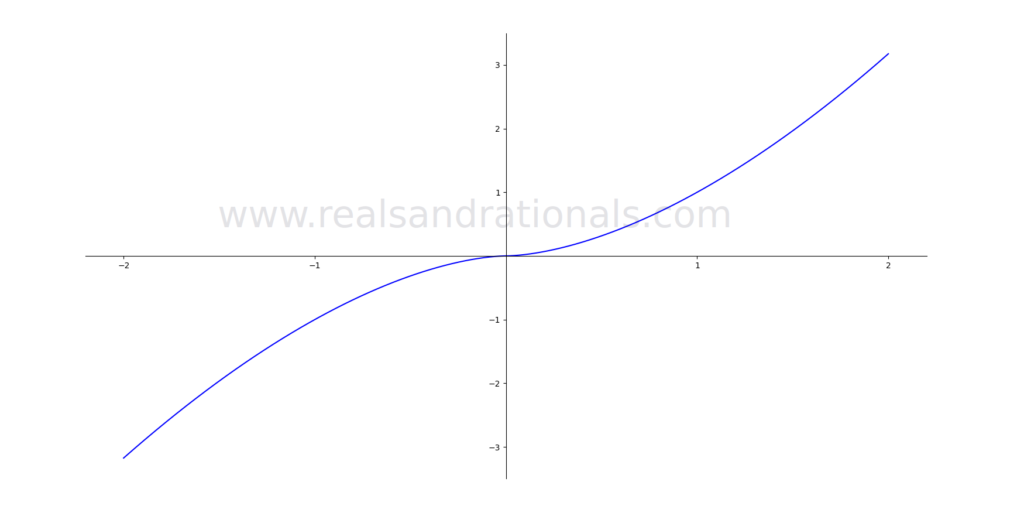
Identify where each of the following functions is differentiable.
. (Here,
denotes the greatest integer that is less than or equal to
. For example,
,
and
)
Problem set
- What is the slope of tangent to the graph of
at
?
- What is the slope of tangent to the graph of
at
?
- What is the slope of tangent to the graph of
at
?
- What is the slope of tangent to the graph of
at
?
- What is the slope of tangent to the graph of
at
?
Problem set
- Give the equation to the tangent to the graph of
at
.
- Give the equation to the tangent to the graph of
at
.
- Give the equation to the tangent to the graph of
at
.
Power rule, Sum rule, product rule and quotient rule
Exercises
Problem set
In each of the following problems, a function is given. In each case, find
.
Problem set
In each of the following problems, a function is given. In each case, find
.
Problem set
Find the derivative of each of the following functions.
Problem set
Find the derivative of each of the following functions.
Trigonometric, exponential and logarithmic functions
Exercises
Problem set
Find the derivative of each of the following using the definition of derivative.
Problem set
Find the derivative of each of the following functions.
Problem set
Find the derivative of each of the following functions.
Problem set
Prove the following.
Problem set
Find the derivative of each of the following functions.
Chain rule
Exercises
Problem set
Find the derivative of each of the following functions.
Problem set
Find the derivative of each of the following functions.
Problem set
Find the derivative of each of the following functions.
Problem set
Find the derivative of each of the following functions.
Problem set
Find the derivative of each of the following functions.
Problem set
Justify the following.
Implicit differentiation
Exercises
Problem set
Find the derivatives for the following at the given points.
, at
, at
, at
, at
and
, at
, at
Derivative of inverse of a function
Exercises
Problem set
- Given that
and
is a point on the graph of
, find the value of
.
- Given that
and
is a point on the graph of
, find the value of
.
Problem set
Identify domain and range for each of the following functions, and obtain their derivatives.
Problem set
Justify the following.
Problem set
Justify the following.
Antiderivatives
Exercises
Problem set
Find an antiderivative for each of the following.
Problem set
Find an antiderivative for each of the following.