Motivation and intuition
Exercises
Problem set
- Consider the function
. Make a function table to find the values of
at
. Look for a pattern in the values of
as
gets closer and closer to
. Based on the pattern, determine the value of
.
- Consider the function
. Make a function table to find the values of
at
. Look for a pattern in the values of
as
gets closer and closer to
. Based on the pattern you observe, determine the value of
.
- Consider the function
. Make a function table to find the values of
at
. Look for a pattern in the values of
as
gets closer and closer to
. Based on the pattern you observe, determine the value of
.
- Consider the function
. Determine the values of
at
. Look for a pattern in the values of
as
gets closer and closer to
. Based on the pattern you observe, determine the value of
.
- Consider the function
. Determine the values of
at
. Look for a pattern in the values of
as
gets closer and closer to
. Based on the pattern you observe, determine the value of
.
- Consider the function
. Determine the values of
at
. Look for a pattern in the values of
as
gets closer and closer to
. Based on the pattern you observe, determine the value of
.
- Consider the function
, where
takes values in radians. Determine the values of
at
. Look for a pattern in the values of
as
gets closer and closer to
. Based on the pattern you observe, determine the value of
.
- Consider the function
, where
takes values in radians. Determine the values of
at
. Look for a pattern in the values of
as
gets closer and closer to
. Based on the pattern you observe, determine the value of
.
Problem set
- For the function shown in the graph, evaluate the limits.
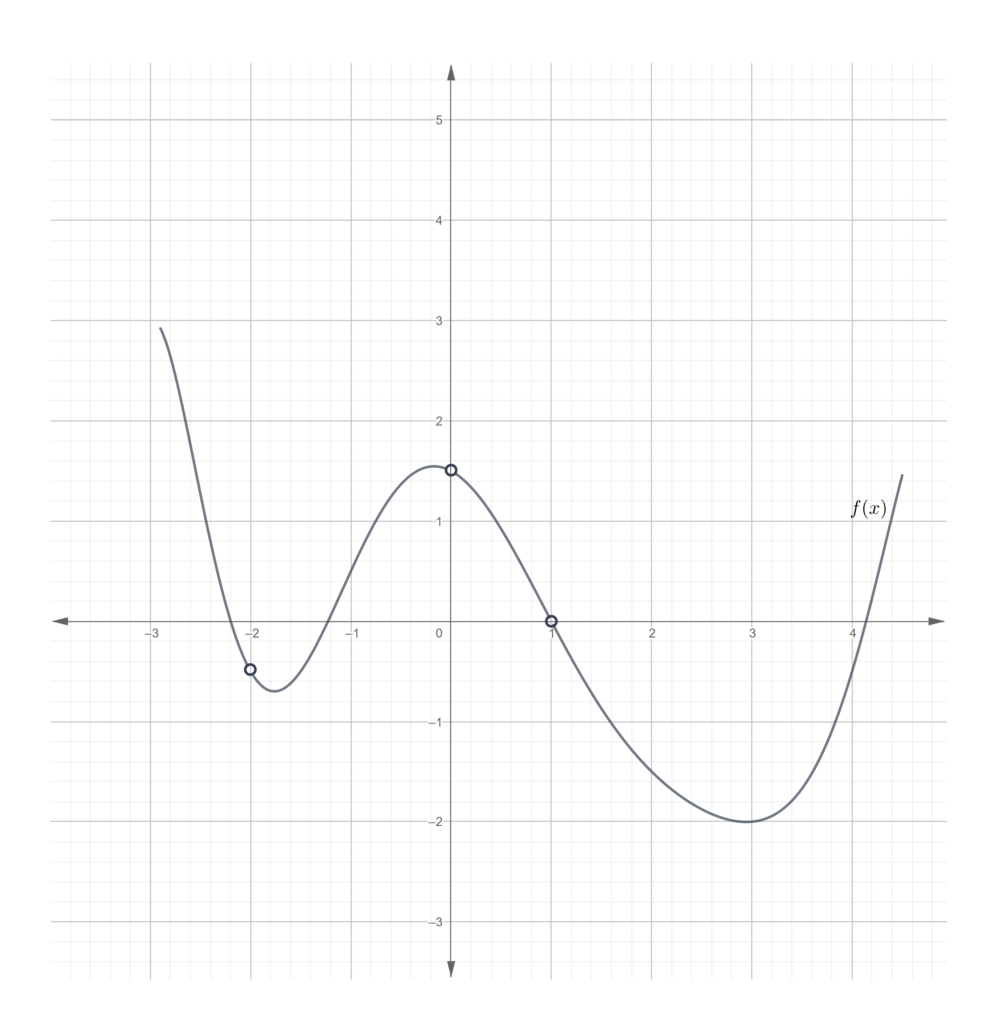
- For the function shown in the graph, evaluate the limits.
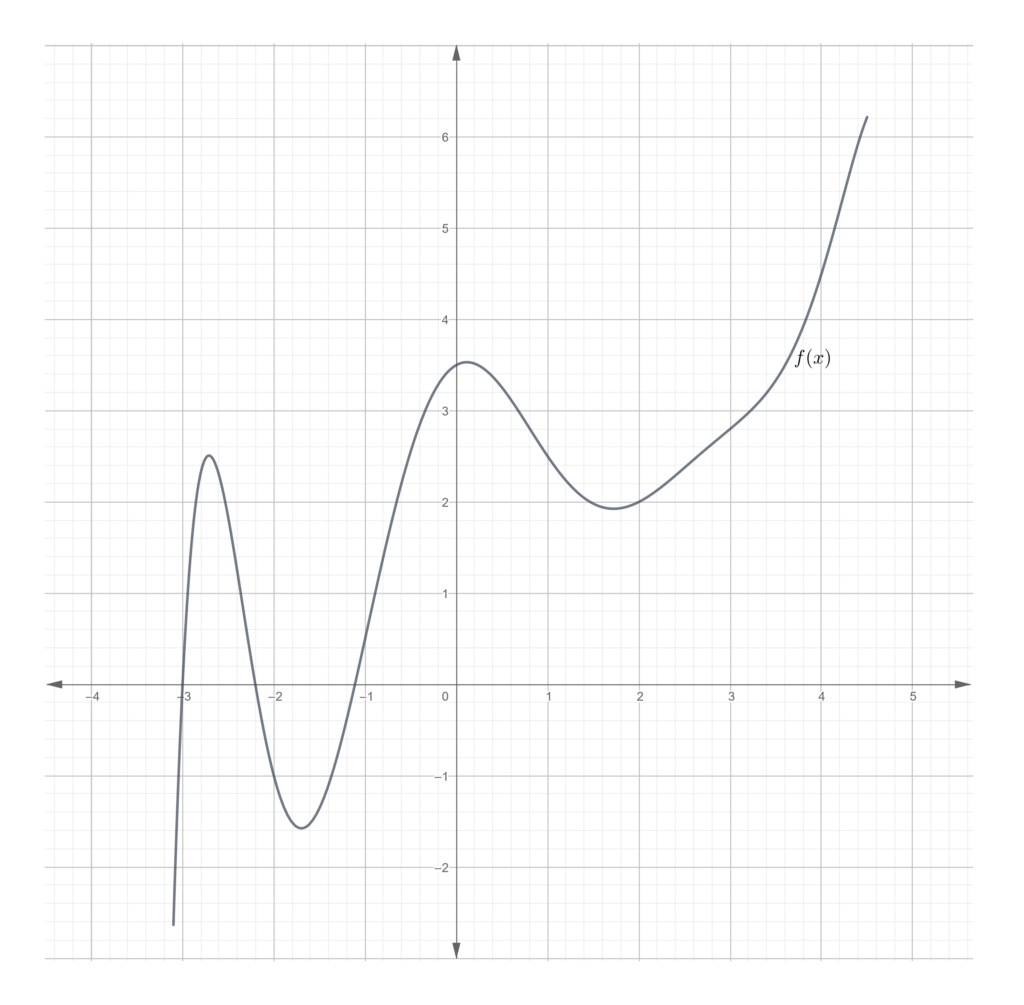
- For the function shown in the graph, evaluate the limits.
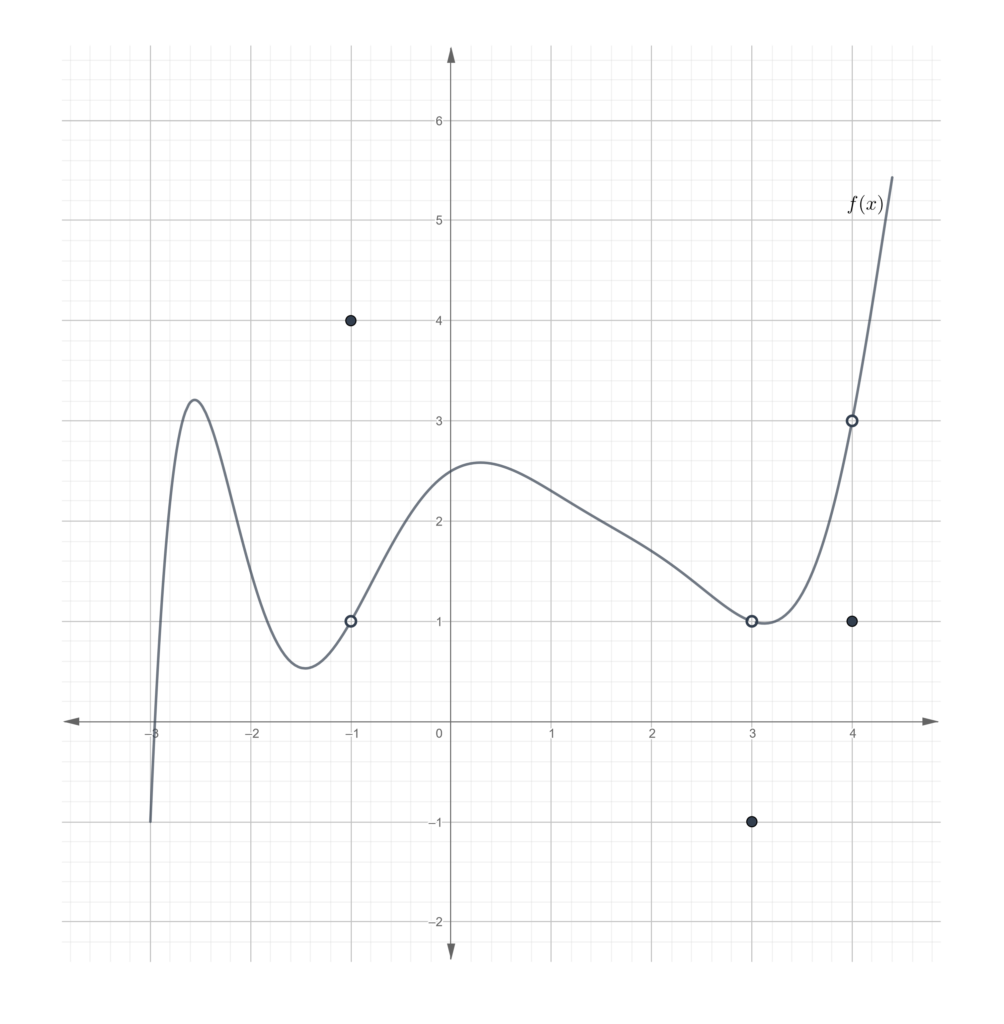
- For the function shown in the graph, evaluate the limits.
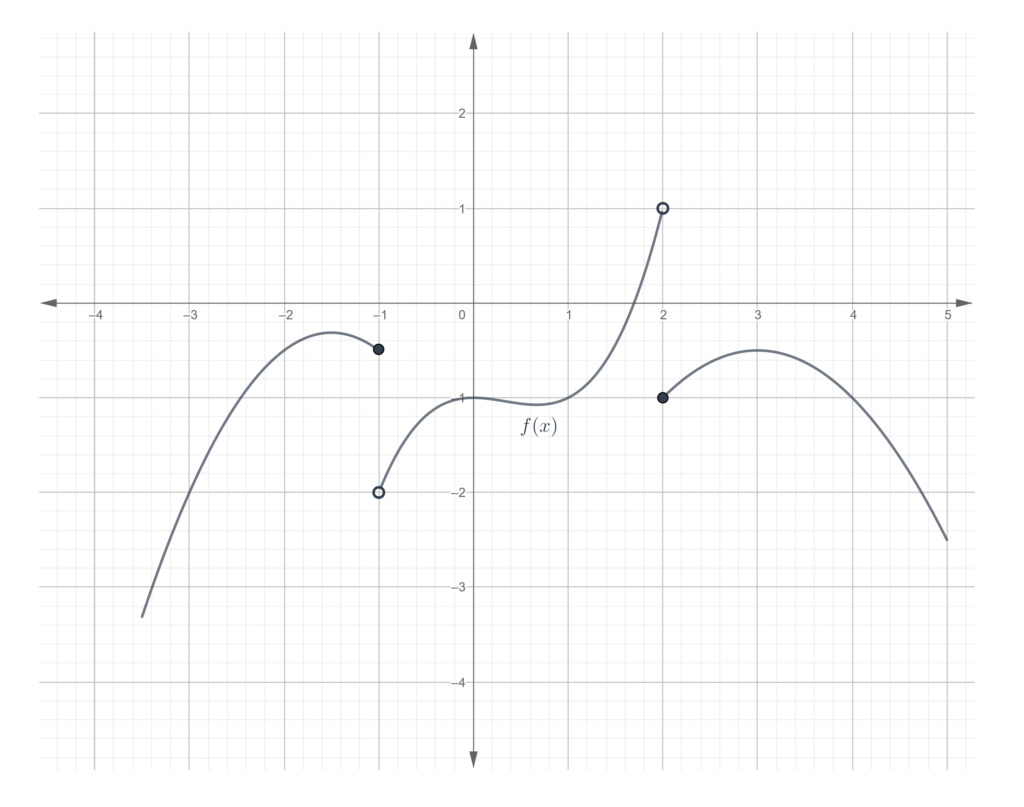
Problem set
- Consider the polynomial
. We consider a sequence of five secants to this polynomial. Note that a secant intersects the graph of the polynomial at two points. For all the secants that we consider, one of the points of intersection has
-coordinate equal to
. The secants differ from each other in their second points of intersection. The
-coordinates for the second points of intersection of the five secants are respectively as follows:
.
- Find the slope of each of the five secants.
- Can you now guess the slope of the tangent to the polynomial at
?
- When a function is drawn on the coordinate plane, a relevant question to ask is how much the area between the curve representing the function and the X-axis is. This is often referred to as the area under the curve. In this problem, we will approximately calculate the area under the curve for the function
between
and
. We do this approximation by constructing rectangles to cover the area under the curve. We do this in multiple stages, where the number of rectangles we construct in each consecutive stage doubles. As the number of rectangles increases, the top end of the rectangle aligns better with the curve (see the figures below), and the sum of the areas of rectangles approximates the area under the curve better.
- Find the sum of areas of rectangles in the following figure.
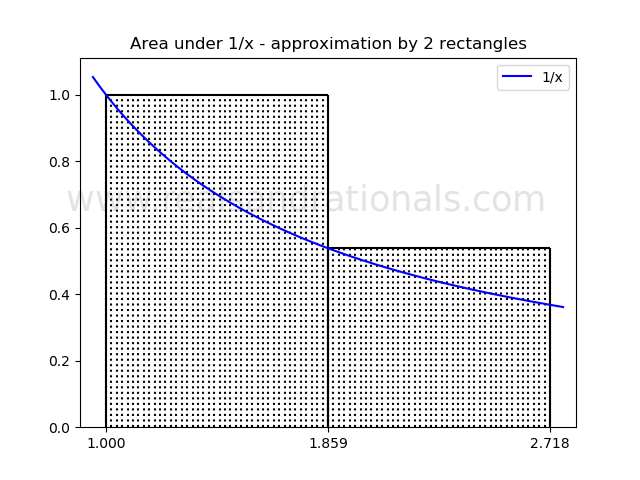
- Find the sum of areas of rectangles in the following figure.
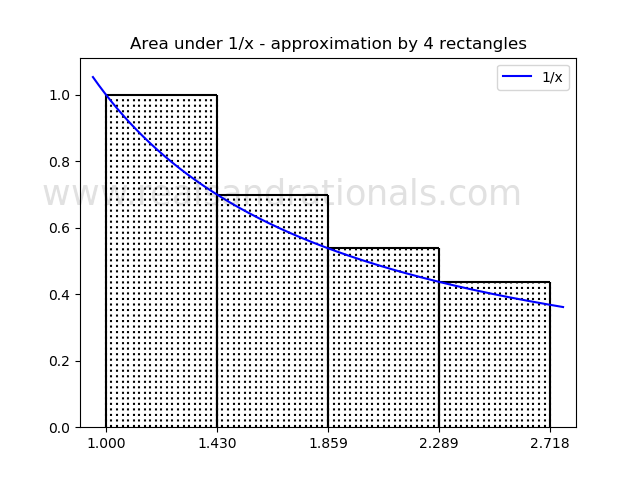
- Find the sum of areas of rectangles in the following figure.
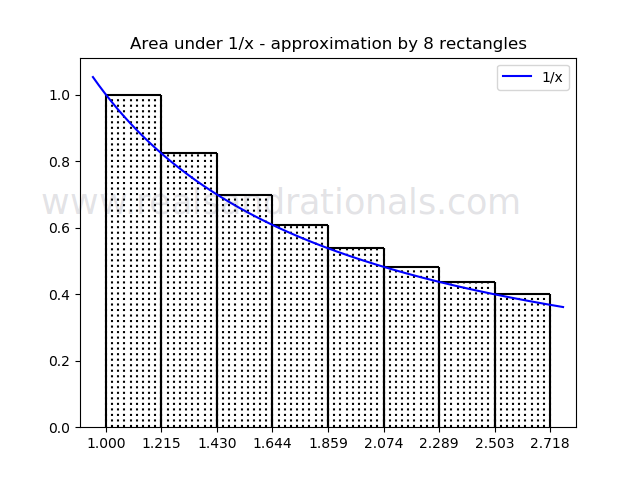
- Find the sum of areas of rectangles in the following figure.
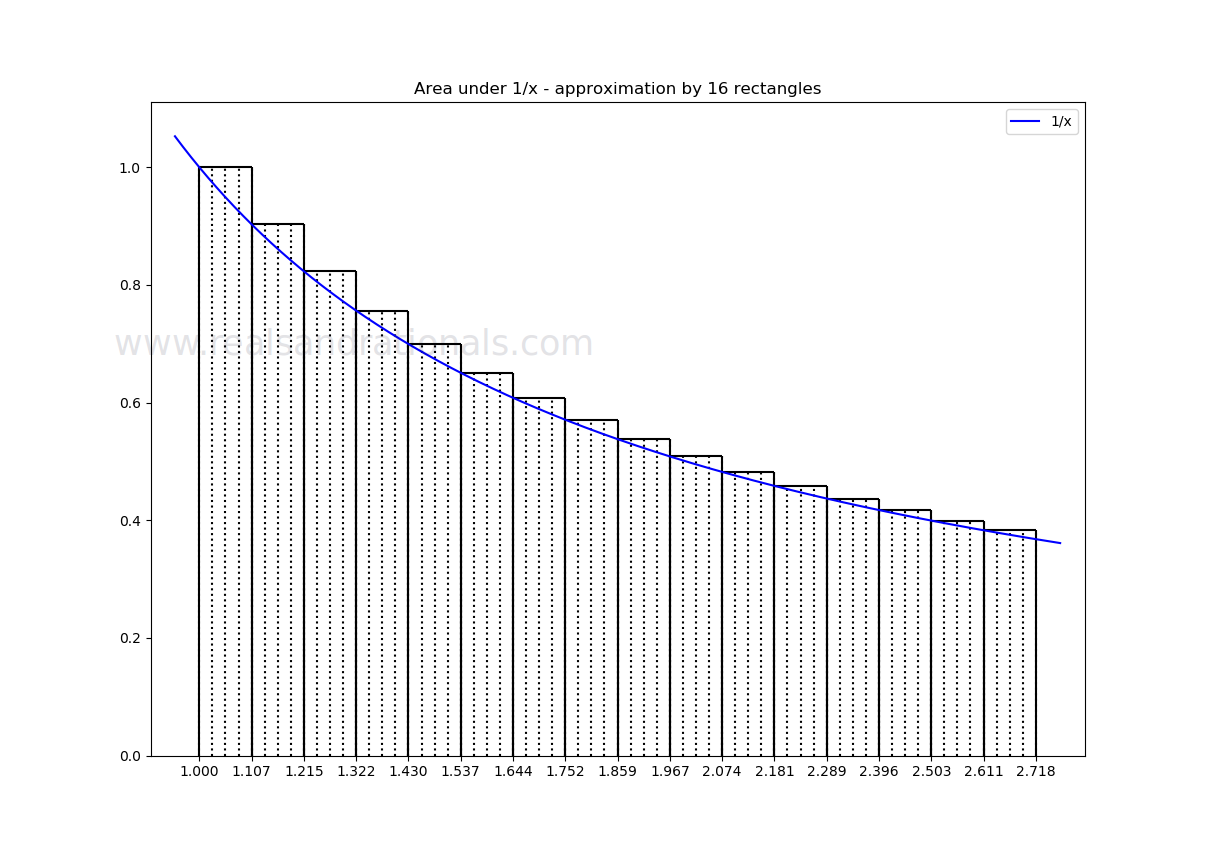
- Can you now estimate the area under the curve
between
and
?
- Find the sum of areas of rectangles in the following figure.
Continuity
Exercises
Problem set
Identify whether each of the following functions is continuous or discontinuous. If discontinuous, identify the points of discontinuity
Problem set
Identify whether each of the following functions is continuous or discontinuous. If discontinuous, identify the points of discontinuity
Problem set
Explain with reasons whether each of the following functions is continuous or discontinuous. If discontinuous, identify the points of discontinuity
Problem set
Explain with reasons whether each of the following functions is continuous or discontinuous. If discontinuous, identify the points of discontinuity
Problem set
Evaluate the following limits
Problem set
Evaluate the following limits.
Problem set
Say, we have the following function definitions:
Based on the above, evaluate the following.
and
and
and
and
and
Problem set
Evaluate the limits in each of the following problems.
Note that, is the smallest integer that is greater than or equal to
. For example,
. And,
is the greatest integer that is less than or equal to
. For example,
.
Problem set
Evaluate the following limits
Limit laws
Exercises
Problem set
Evaluate the following limits
Problem set
Evaluate the following limits
Problem set
Evaluate the following limits
Limits involving trigonometric functions
Exercises
Problem set
Evaluate the following limits
Problem set
Evaluate the following limits
Problem set
Evaluate the following limits
Problem set
Evaluate the following limits
Problem set
Evaluate the following limits
Problem set
Evaluate the following limits
Epsilon-delta definition
Exercises
Problem set
- If
, find
such that
whenever
.
- If
, find
such that
whenever
.
- If
, find
such that
whenever
.
- If
, use a calculator to find
such that
whenever
.
Problem set
Justify the following using the definition of a limit.
Limits involving infinity
Exercises
Problem set
Evaluate the following limits
Problem set
Evaluate the following limits
L’Hopital’s rule
For Zero over zero form
Exercises
Problem set
Evaluate the following limits
Problem set
Evaluate the following limits
For infinity over infinity form
Exercises
Problem set
Evaluate the following limits
Problem set
Evaluate the following limits
Problem set
Evaluate the following limits
For other indeterminate forms
Exercises
Problem set
Evaluate the following limits
Problem set
Evaluate the following limits