Coordinate plane
Exercises
Problem set
In the coordinate plane below, several points are marked.
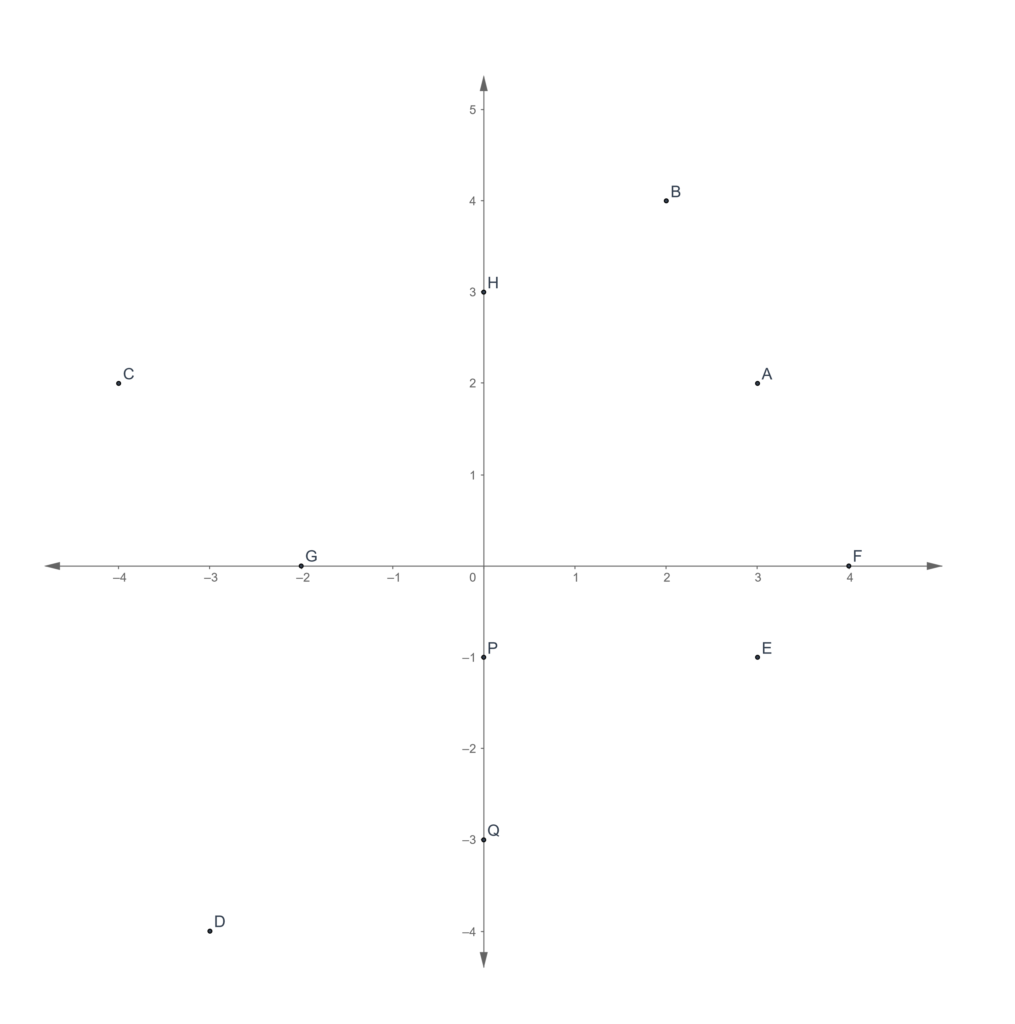
For each of the problems below, give the coordinates of the named point.
Problem set
For each of the following problems, draw -axis and
-axis to represent a coordinate plane. Then, mark each of the following points on a coordinate plane.
Problem set
For each of the following pairs of points, find the distance between the points.
Problem set
For each of the following pairs of points, find the distance between the points.
Slope of a straight line
Exercises
Problem set
- Can there be two different straight lines going through the same point?
- Can there be two different straight lines having the same slope?
- Can there be two different straight lines having the same slope and the same y-intercept?
- Can there be two different straight lines having the same slope and the same x-intercept?
Problem set
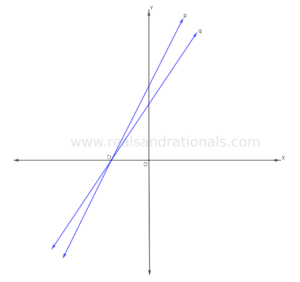
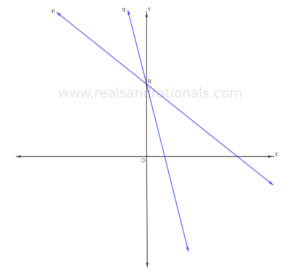
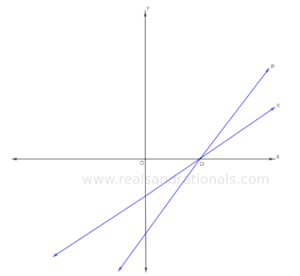
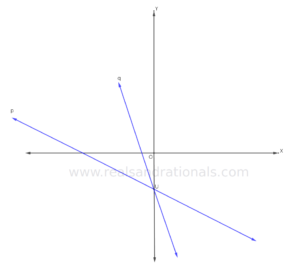
In each of the following problems, identify which of the two lines graphed in blue has bigger slope.
Problem set
- A ladder leaning against a wall reaches a window that is
m high. The foot of the ladder is
m away from the wall. What is the slope of the ladder in its current position?
- A kid goes up a vertical ladder of height
to reach the top of a slide. After sliding down, the kid needs to walk
to begin climbing up the ladder again. What is the slope of the slide?
- A vertical post of height
m is held in place by a rope going from the top of the post to the ground. The rope makes an angle with the vertical post, and the point where the rope is tied to the ground is
m away from the foot of the vertical post. What is the slope of the rope?
- A ladder is leaning against a tree with a slope of
to reach a branch of the tree. If the foot of the ladder is
units from the base of the tree, how high is the branch?
- A ladder is used to hang an art piece
high on a wall. The foot of the ladder is
away from the wall. A second ladder is used to hang another art piece
high on the wall, and its foot is
away from the wall. Which ladder is in a steeper position?
- A ladder of length
is leaning against a wall to reach an art piece
high. What is the slope of the ladder in its current position?
- A rope of length
is used to anchor a flag post of length
to the ground. What is the slope of the rope?
Problem set
What is the slope of the line going through the following pairs of points?
Problem set
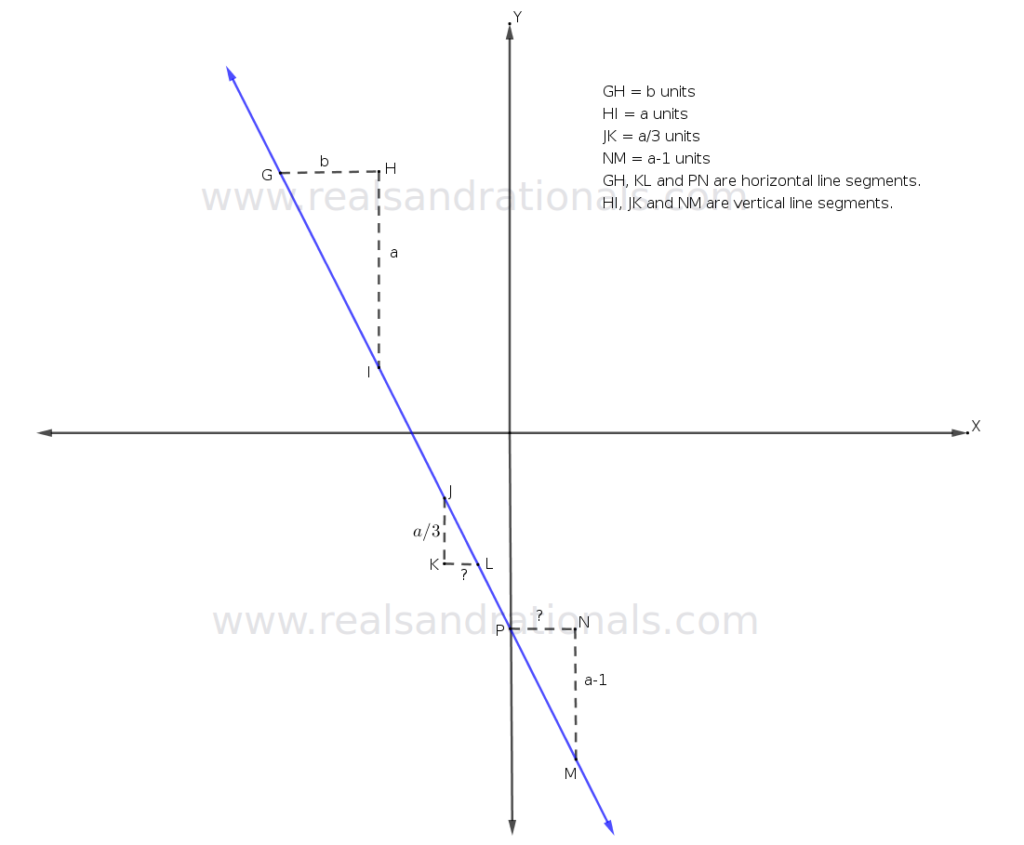
- In the following figure, a straight line is graphed in blue. Using the information shown in the figure, find the values of
and
in terms of
and
.
X-intercept and Y-intercept
Exercises
Problem set
- Can there be two different lines having the same y-intercept?
- Can there be two different lines having the same x-intercept?
- Can there be two different lines going through the same two points?
- Can there be two different lines having the same x-intercept and the same y-intercept?
Problem set
- What is the
-intercept of the line going through
and
?
- What is the
-intercept of the line going through
and
?
- What is the
-intercept of the line going through
and
?
- What is the
-intercept of the line going through
and
?
Equation of a straight line
Exercises
Problem set
-
is a line with slope
and a
-intercept of
. If
is a point on the line
, find the value of
.
-
is a line with slope
and a
-intercept of
. If
is a point on the line
, find the value of
.
-
is a line with slope
and a
-intercept of
. If
is a point on the line
, find the value of
.
-
is a line with slope
and a
-intercept of
. If
is a point on the line
, find the value of
.
-
is a line with slope
and a
-intercept of
. If
is a point on the line
, find the value of
.
-
is a line with slope
and a
-intercept of
. If
is a point on the line
, find the value of
.
Problem set
In each of the following graphs, the X-axis and the Y-axis are drawn to the same scale.
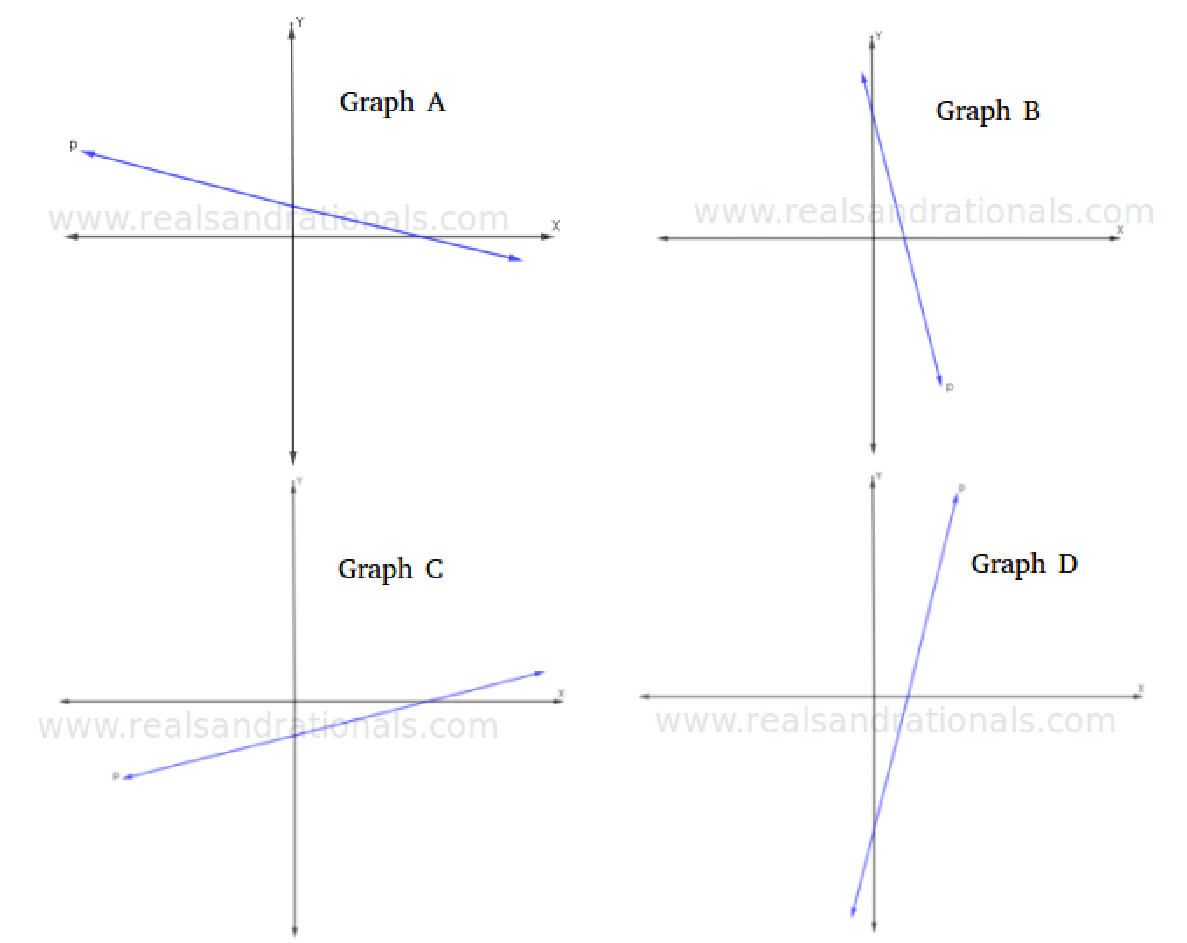
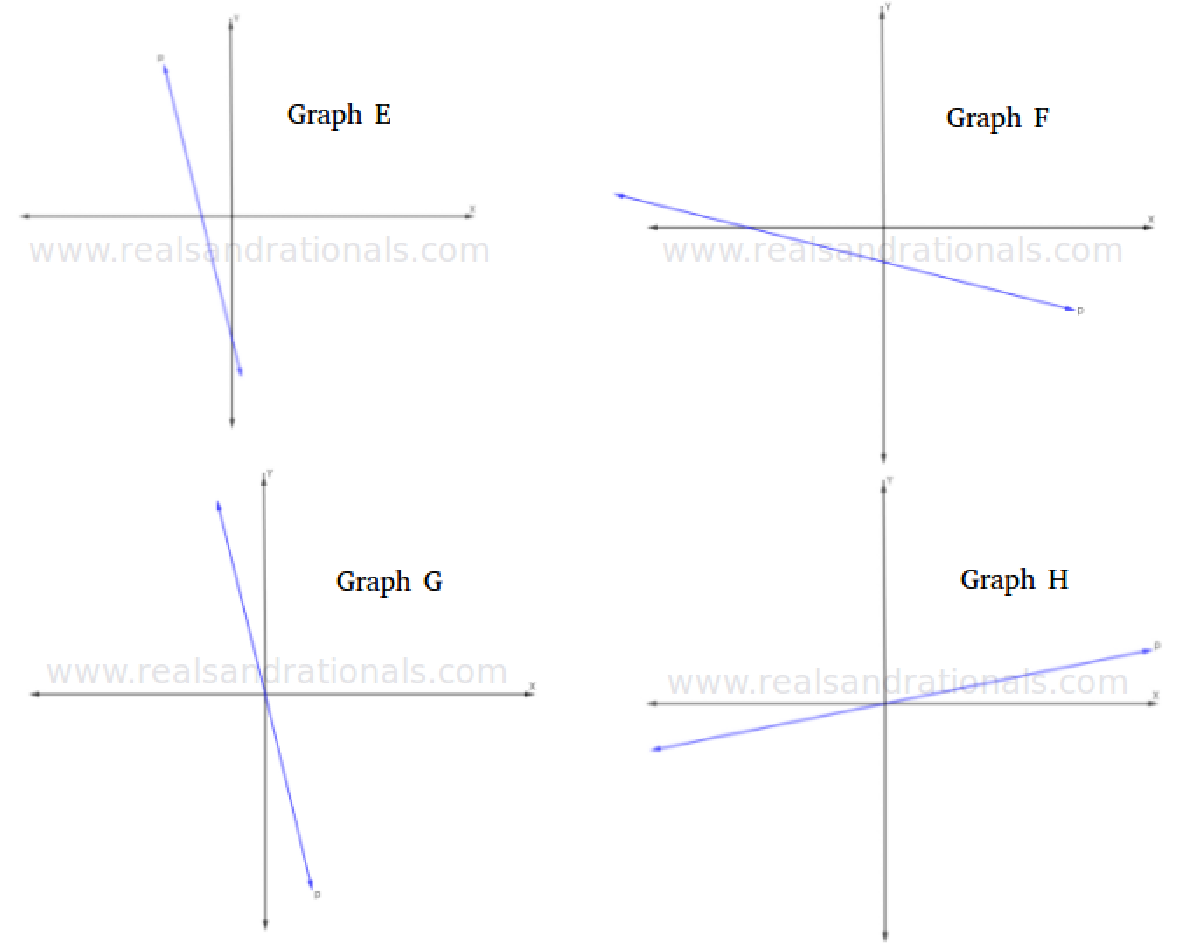
Identify which of the above graphs is represented by each of the following equations.
Problem set
- What is the equation of a line that has slope
and that goes through point
?
- What is the equation of a line that has slope
and that goes through point
?
- What is the equation of a line that has slope
and that goes through point
?
- What is the equation of a line that has slope
and that goes through point
?
- What is the equation of a line that has slope
and that goes through point
?
- What is the equation of a line that has slope
and that goes through point
?
Problem set
- What is the equation of a line that goes through
and
?
- What is the equation of a line that goes through
and
?
- What is the equation of a line that goes through
and
?
- What is the equation of a line with y-intercept
and x-intercept
?
- What is the equation of a line with slope
and that goes through point
?
- What is the equation of a line with slope
and x-intercept
?
- What is the equation of a line with slope
and x-intercept
?
Problem set
Determine the slope, -intercept and
-intercept for each of the following lines.
Problem set
- What is the equation of a horizontal line that is
units above
-axis?
- What is the equation of a horizontal line that is
units below
-axis?
- What is the equation of
-axis?
- What is the equation of a vertical line that is
units to the right of
-axis?
- What is the equation of a vertical line that is
units to the left of
-axis?
- What is the equation of
-axis?
Problem set
Which of the following equations represent straight lines? If an equation represents a line, identify its slope, -intercept and
-intercept.
Intersecting and parallel lines
Exercises
Problem set
- What is the equation of a line parallel to
that goes through the point
?
- What is the equation of a line parallel to
that goes through point
?
- What is the equation of a line parallel to
with y-intercept
?
- What is the equation of a line perpendicular to
that goes through
?
- What is the equation of a line perpendicular to
that goes through the origin?
Problem set
Determine the point of intersection for each of the following pairs of lines.
,
,
,
,
,
,
such that
, the line going through
and
, the line going through
and
,
,
Problem set
- In the following figure, two parallel lines are shown in blue on a coordinate plane.
- If
units, express
in terms of
and
.
- if
units, express
in terms of
and
.
- if
units, express
in terms of
and
.
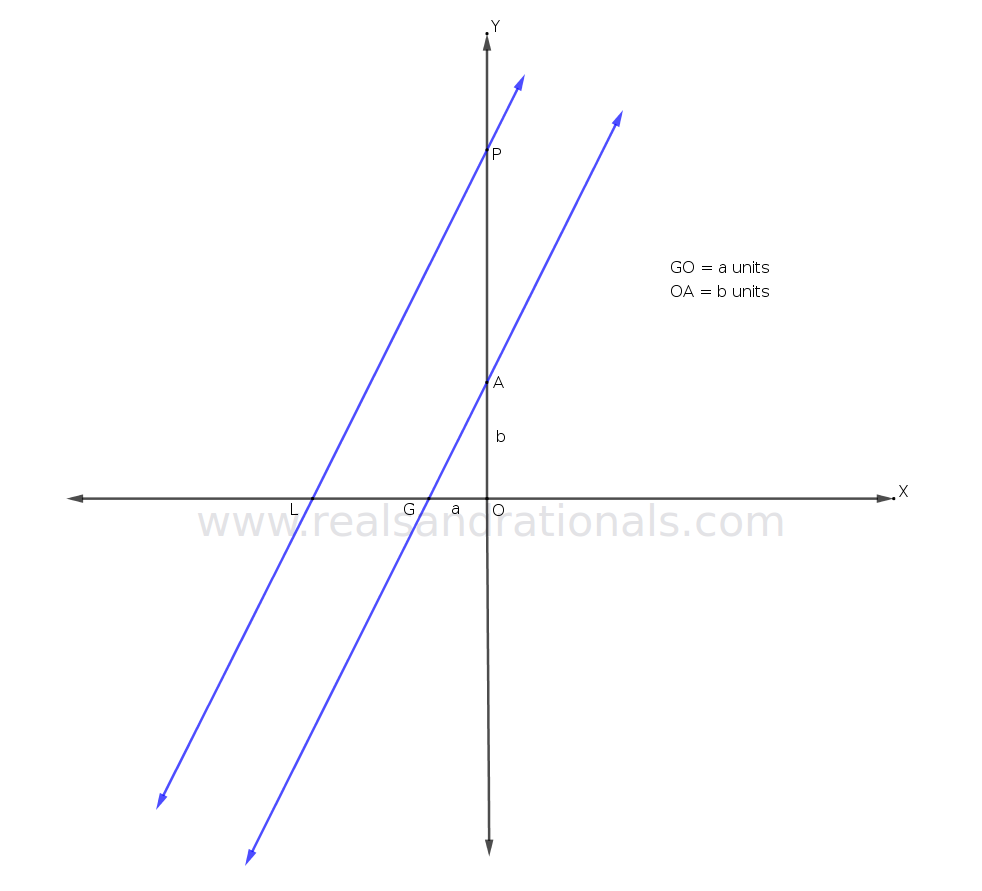
- If
- In the following figure,
is a parallelogram. The points
and
lie on the
-axis. Equation of
is
and equation of
is
. What are the equations of
and
?
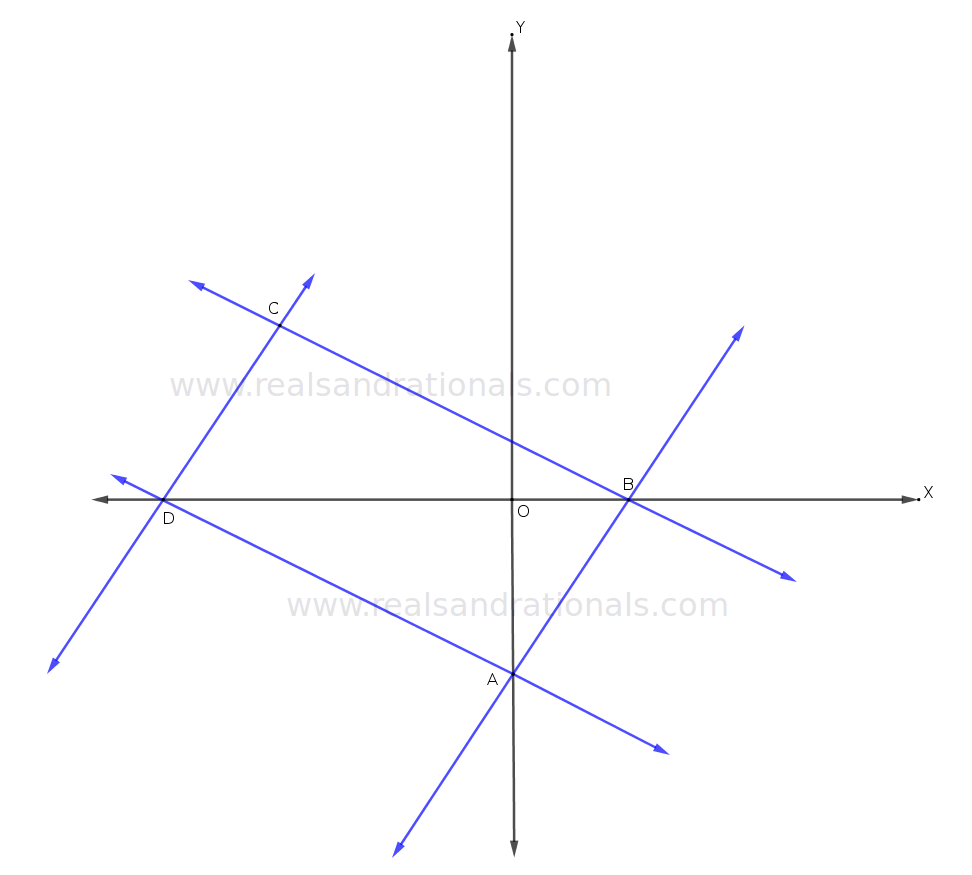
is a parallelogram. The points
are
respectively. What is the point
?
Problem set
In the following figure, two parallel lines are graphed in blue.
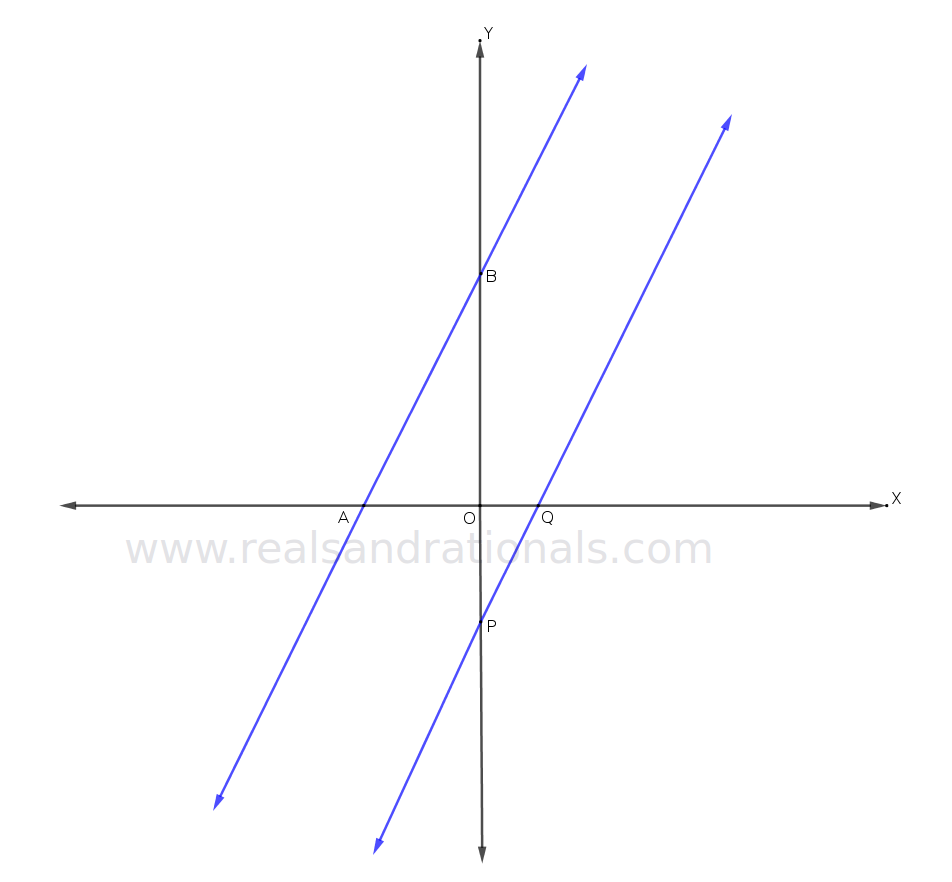
The following questions are based on the above figure.
- If
and
, what is the value of
?
- If
and
, what is the value of
?
- If
and
, what is the point
?
- If
and
, what is the equation of the line
?
- If
and
, what is the equation of line
?
Distance between points
Exercises
Problem set
What is the distance between the following pairs of points?
Problem set
What is the distance between the following pairs of points?
- What is the formula for distance between two points
and
?
- Does
represent a line? What is its y-intercept? Find points on the line that are at a distance of
units from its y-intercept.
- Does
represent a line? Find equations of the two lines parallel to this line at a perpendicular distance of
units from it.
- Does the equation
represent a line? If so, write in standard form. What is its y-intercept? Observe that this line passes through the origin. Find points on the line that are
units away from the origin.
Miscellaneous
Exercises
Problem set
are two diagonal end points of a rectangle. One of the sides of the rectangle is horizontal. Find all the vertices of the rectangle.
are two diagonal end points of a rectangle. Two of the vertices of the rectangle lie on the Y-axis. Find the area of the rectangle.
are the three vertices of a triangle. The area of the triangle is
square units. What are the possible values of
?
are the three vertices of a triangle. The area of the triangle is
square units. What are the possible values of
?
Problem set
- Are
colinear?
- Are
colinear?
- Are
colinear?
are colinear. What is the value of
?
are colinear. What is the value of
?
Problem set
Which of the following points lie on the graph of the equation ?
Problem set
- A circle of radius
unit has origin as its center. Identify its
-intercepts and
-intercepts.
- What is the equation of the line that is perpendicular to
and that goes through the point
?
- What is the y-intercept of the line with slope
and x-intercept
?
- A line goes through the points
and
. Find a point on the line that is to the left of the vertical line
.
- A line with slope
and
-intercept
is translated horizontally to the left by
units. What is the
-intercept of the new line generated?