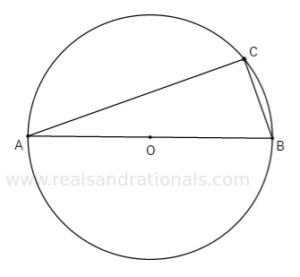
- In the following figure,
is the center of the circle, and
is a diameter of the circle. Prove that
.
In this problem set, two concentric circles are shown in the figures. is the center of the circles.
- In the following figure, prove that
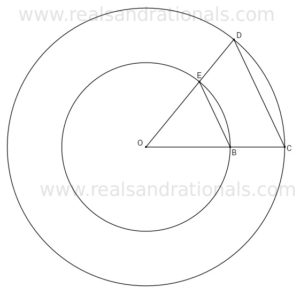
- In the following figure, prove that
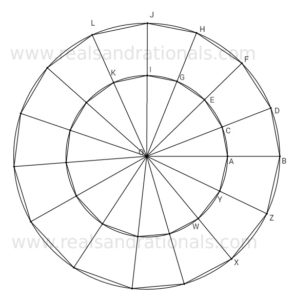
- In the figure above, prove that
.
- In the figure above, prove that
.
- In the figure above, prove that
.
- In the figure above, prove that
.
- Do you see how
?
- Do you see how
?
- Do you see how
?