Congruence
Exercises
Problem set
For each of the following problems, assume there are two triangles and
, and using the information given, answer with justification whether the two triangles are congruent or not.
Problem set
For each of the following problems, assume there are two triangles and
, and using the information given, answer with justification whether the two triangles are congruent or not.
Problem set
- In
,
. Further,
is a point on
such that
and
. What is the measure of
?
- In
,
. Further,
is a point on
such that
and
. What is the measure of
?
- In
,
. Further,
is a point on
such that
and
. What is the measure of
?
Problem set
- In
,
and
. And,
is the mid-point of side
so that
. Then,
is a point on
such that
. What is the measure of
?
Angle and side relations
Exercises
Problem set
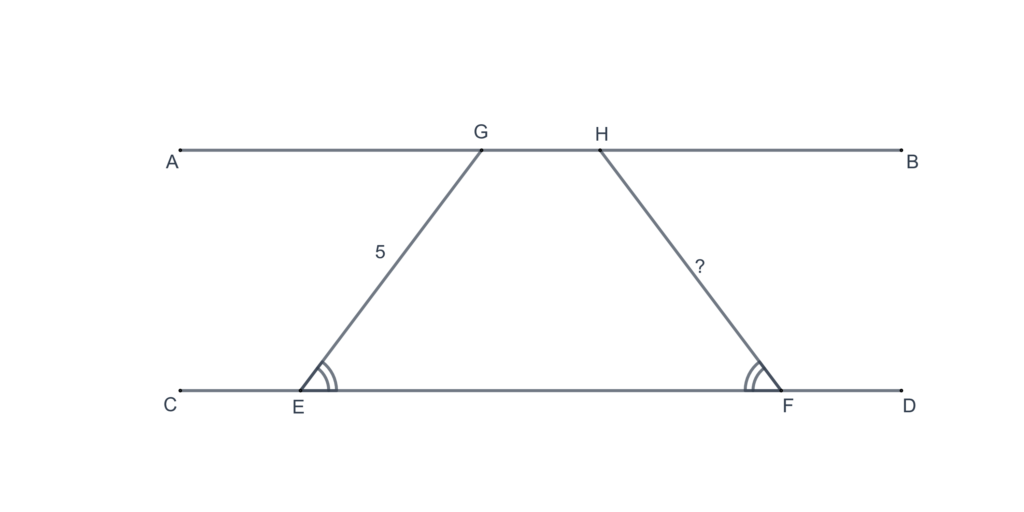
- Prove that in a triangle, if two angles are congruent, the sides opposite to them are also congruent.
- Prove that in a triangle, if two sides are congruent, the angles opposite to them are also congruent.
- Which of the following are possible in a triangle?
- Which of the following are possible lengths of sides of a triangle?
, given that
- Two sides of a triangle are
and
. What are the smallest and the largest possible lengths for the third side of a triangle?
Miscellaneous
Exercises
Problem set
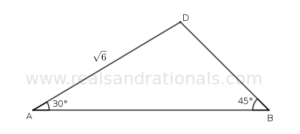
- In the following figure,
. If
, justify that
.
- In the following figure,
is a right angle. And,
and
are squares.
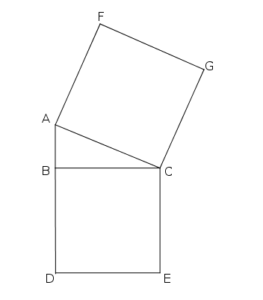
Area of squareis
square units, and area of square
is
square units. What is the area of
?
- Area of an equilateral triangle
is
square units.
is another equilateral triangle whose side is one-third of the side of
. What is the area of
?
- In the following figure,
and
are straight line segments.
and
. What is the area of the parallelogram
?
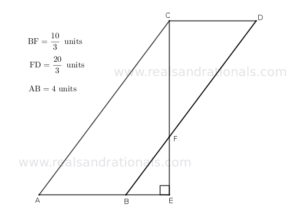
- In the above problem, what is the area of the polygon
?
- In the following figure
is a parallelogram, and
is the point of intersection of diagonals
and
. What is the area of
?
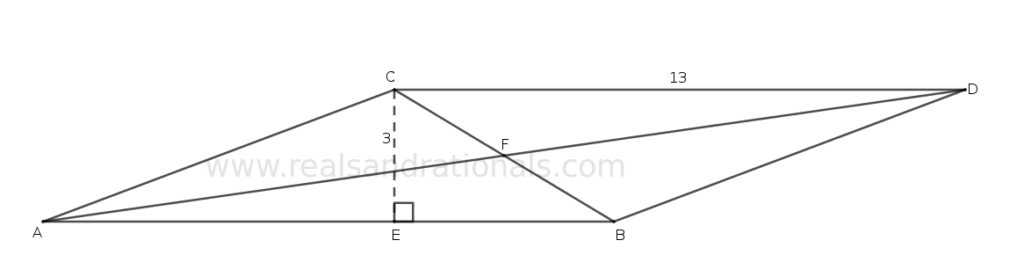
Problem set
- In the following figure, what is the area of the
?
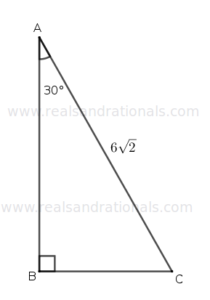
- In the following figure, what is
?
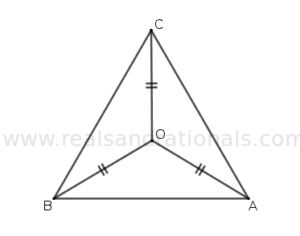
- In the following figure, what is the area of
?
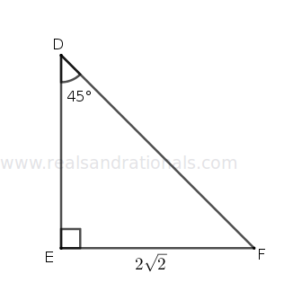
- In the following figure, what is the area of
?
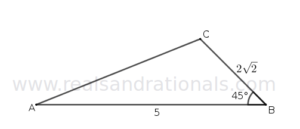
- In the following figure, what is the area of
?
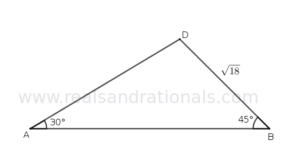
- In the following figure, what is the area of
?