Learn – Math circle – Fun problems

Problem set 1
Problem set 2
Problem set 3
Problem set 4
Problem set 5
Problem set 6
Problem set 7
Problem set 8
Problem set 9
Problem set 10
Problem set 11
Problem set 12
Problem set 13
Problem set 14
Problem set 15

Problem set 1

If a natural number $n$ leaves a remainder of $33$ when divided by $100$ , what remainder does the number $n + 80$ leave when divided by $100$ ?
In the repeating decimal, $32.82\overline{35729}$ , what is the $6843$ rd digit after the decimal point?
What is the value of: $1000+1001+1002+\cdots+1198+1199+1200$ ?
$\frac{2}{7} < \frac{x}{8} < \frac{3}{7}$ . What whole number value can replace $x$ ?
I distribute $90$ grapes into $9$ bowls. Each bowl has a different number of grapes, and no bowl has a number of grapes that is a multiple of $3$ . What is the greatest number of grapes that can be in a bowl?

Problem set 2

You get $85$ days of summer holidays. What is the maximum number of Thursdays that can be there during the holidays?
From a bag of candies, Don takes half the candies. Alice takes half of what are left after Don. Jim takes half of what are left after Don and Alice. Anita takes half of what are left after Don, Alice and Jim. Finally, Rachel takes half of what are left. In the end, three candies are left in the bag. How many candies were in the bag to start with?
Oliver has twice as many brothers as he has sisters. His sister Rita has three times as many brothers as she has sisters. How many boys and girls (excluding parents) are there in all in the family?
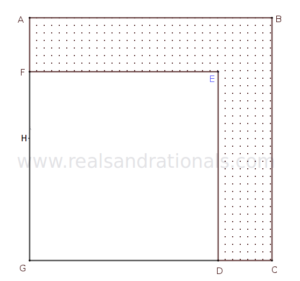
In the following figure, $ABCG$ and $FEDG$ are squares each with a counting number as the length of its side. The area of the dotted region is $32$ square units. $H$ is the midpoint of the side $AG$ . What is the length of $AH$ ?
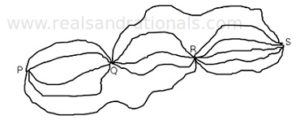
How many different paths are there to go from point $P$ to point $S$ such that points $P, Q, R$ and $S$ are visited once and only once?

Problem set 3

How many numbers between $500$ and $1000$ can be written as a product of an even number times an even number?
The number $2310$ can be written as a product of prime numbers as $2310 = 2\times 3\times 5\times 7\times 11$ . How many different factors does $2310$ have?
Sylvia has $9$ candies more than Lydia. Sylvia gives $12$ of her candies to Lydia. Now, how many more candies does Lydia have than Sylvia?
The number of stamps in Raman’s stamp collection is between $60$ and $160$ . He arranges the stamps in groups of $6$ , and he finds that two stamps are left over after he forms the groups. He arranges them in groups of $5$ , and he finds that he has one stamp left over. He arranges them in groups of $4$ , and he finds that there are no stamps left over after he forms the groups. How many stamps does Raman have in his collection?

Problem set 4

represents a three digit number key. Following are clues to decode the key:
- In the arrangement $5.8.6$ , two digits are incorrect, one digit is correct. The correct digit is however in the wrong place.
- In the arrangement $7.8.9$ , two digits are incorrect, one digit is correct. And, the correct digit is in the correct place.
- In the arrangement $8.7.4$ , two digits are correct, one digit is incorrect. And, both the correct digits are in the wrong places.
What is the three digit number key?
Jay has two boxes. The first box holds numbers , while the second box holds numbers . He does the following with the numbers:
1. he pairs up each number in the first box to a number in the second box. For example, he could pair up the numbers as $(6,4), (7,5), (8,3), (9,2)$ . Note that each of the numbers is used only once in forming the pairs.
2. Once he forms the pairs, he multiplies the numbers in each pair. Thus, in the above example, he does $6\times 4$ to get $24$ , $7\times 5$ to get $35$ and so on.
3. he then adds the four resultant numbers to get one final number.
What is smallest number he could get by doing the above steps using the numbers he has?
$101\times 101 + 101\times 102 + 101\times 103 +\cdots+101\times 201 = ?$
In a sequence of numbers, the first number is $2$ and the third number is $7$ . The sequence is such that the sum of any three consecutive numbers is $13$ . What is the thousandth number of the sequence?
A train covers a distance of $2$ miles in $45$ sec. How many miles does the train cover in $2$ hours?

Problem set 5

If $|a| - 1 = 1$ , what are all the possible values of $a$ ?
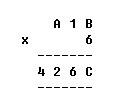
In the following multiplication, different letters represent different digits. What is the value of the three digit number $ABC$ ?

Mr.Sun, Mr.Mercury, Mr.Earth and Mr.Neptune are strolling in a garden. Mr.Sun says he is older than Mr.Earth. Mr.Earth says he is older than Mr.Mercury. Mr.Mercury says he is older than Mr.Earth. Mr.Neptune says he is older than Mr.Sun, but younger than Mr.Mercury. All but one are saying the truth. Who is lying?
To paint the surface of a cube of side $2$ cm, $12$ ml of paint is required. Ten such unpainted cubes are taken, stacked on top of each other and glued together. How much paint is required to paint the surface of this new structure?

Problem set 6

At exactly 3:30PM, Will started hiking up a trail while Arthur started hiking down the same trail. By 4:30PM, Will had hiked up two-thirds of the trail, while Arthur had hiked down five-sixths of the trail. What is the distance between Arthur and Will at 4:30PM as a fraction of the trail length?
A whole number $N$ when divided by each of $14, 12$ and $16$ leaves a remainder $1$ each time. What is the smallest possible value for $N$ ?
The least common multiple (LCM) of two numbers is $24$ . One of the numbers is $8$ . What is the total number of possibilities for the other number?
The product of digits of a four digit number is $504$ . What is the biggest possible value for the four digit number?

Problem set 7

Rubik’s cubes of dimensions $3\mbox{ cm }\times 3\mbox{ cm }\times 3\mbox{ cm }$ are being packed in a rectangular box of dimensions $28\mbox{ cm }\times 30\mbox{ cm }\times 10\mbox{ cm}$ . What is the most number of Rubik’s cubes that may be packed in the box?
If $\frac{x^2}{x+x+x+x+x}=1$ , what is the value of $x$ ?
What is the ones place of $123^{123}$ ?
A supervisor has five tasks to be completed, and he has two workers to do the tasks. The five tasks take 4 hours, 5 hours, 6 hours, 10 hours, 12 hours respectively to complete by either of the workers. Assuming the supervisor does not want to split a task between the two workers, what is the shortest time in which he can get all the tasks completed?
What is the number of factors of $72$ ?

Problem set 8

$5$ dozen apples and $4$ dozen oranges together cost $\$46$ . $4$ dozen apples and $5$ dozen oranges together cost $\$44$ . How much do $1$ dozen apples and $1$ dozen oranges together cost? How much does $1$ dozen apples cost?
Carlos spent $\frac{1}{5}$ th of the money he had to buy bread. Of the remaining, he spent $\frac{1}{4}$ th on milk. Of the remaining, he spent $\frac{1}{3}$ rd on eggs. Finally, he had $\$12$ left. How much money did he have to start with?
Ralph’s average score in final exams across all but one of his subjects was $70$ . He now got his score in the last subject as $58$ . This pulled down the average to $67$ . How many subjects did Ralph have in all?
A bus travels $2$ miles in $1$ min $40$ sec. How much distance does the bus travel in $1$ hour?

Problem set 9

An ant is at the number $12$ on the clock. And, the time is exactly $1$ PM now. As the seconds hand moves, the ant moves on the rim of the clock along with the seconds hand. The ant gets tired after moving for $10$ seconds. It starts moving again when the seconds hand makes one complete circle and comes back to the ant. The ant moves again for $10$ seconds, and it takes a break again until the seconds hand makes another complete circle and comes back to it. This same pattern goes on for several minutes. What is the time when the ant first gets to the number $10$ on the clock?
A number is chosen randomly from all two digit numbers. What is the probability that the number is divisible by $5$ ?
Mr.Rumpelstiltskin is between $150$ and $170$ years old. When his age is divided by $4$ , it leaves a reminder of $2$ , and when his age is divided by $10$ , it leaves a reminder of $2$ . What is Mr. Rumpelstiltskin’s age?
The number $n!$ is defined to be $n\times(n-1)\times(n-2)\times\cdots\times3\times 2\times 1$ . For example, $7! = 7\times 6\times 5\times 4\times 3\times 2\times 1$ . What is the value of $\frac{100!}{95!\times 5!}$ ?
What is the smallest number that leaves a remainder $9$ when divided by $10$ , a remainder $10$ when divided by $11$ , a remainder $11$ when divided by $12$ , and a remainder $12$ when divided by $13$ ?

Problem set 10

$A$ represents a digit, and the number $2051AA$ is divisible by $12$ . What is the value of $A$ ?
$100! = 100\times 99\times 98\times \cdots\times 3\times 2\times 1$ . What is the biggest value of $n$ such that $5^n$ is a factor of $100!$ ?
Name the smallest and biggest of the following: $100a, 200a, 300a$ given that $a < 0$
Name the smallest and biggest of the following: $0.1a, 0.01a, 0.001a$ given that $a < 0$
Name the smallest and biggest of the following: $y^2, \sqrt{y}, \frac{1}{y}$ given that $0 < y < 1$

Problem set 11

$a, b, c$ are three numbers such that $a < b < c$ . The average of the three numbers is $2$ more than $b$ . If $b$ is $2$ more than $a$ , how much more than $b$ is $c$ ?
Michael, Ryan, Kevin, David and Sam are standing on a straight line. Ryan is $20$ feet away from Michael, Kevin is $40$ feet away from Ryan, David is $10$ feet away from Kevin, Sam is $15$ feet away from David and Michael is $15$ feet away from Sam. Which two persons are closest in distance to each other, and how far apart (in feet) are they?
We call a number super-duper even (for fun) if it is the sum of six consecutive even numbers. What is the smallest super-duper even number that is bigger than $1000$ ?
What is the value of $100 + 103 + 106 + 109 + \cdots + 997 + 1000$ ?
The average of a certain group of numbers is $1000$ . When the number $898$ is added to the group, the average decreases by $3$ . How many numbers (including the new number added) are there in the group?

Problem set 12

How many numbers between $1000$ and $2000$ leave a remainder of $1$ when divided by $10, 20$ and $30$ ?
A defective clock runs slow, and regularly loses a few seconds every minute. On a particular day, when the correct time was $9:30$ AM, the defective clock showed $9:10$ AM, and when the correct time on the same day was $12:10$ PM, the defective clock showed $11:30$ AM. What time would the defective clock show when the actual time on the same day is $6:50$ PM?
In a room, there are $15$ kids wearing red shirts, $12$ kids wearing green shirts and $20$ kids wearing blue shirts. I call one kid out every minute for $40$ minutes. What is the minimum number of kids wearing red shirts that I know will come out?
Two standard dice are rolled. What is the probability that the sum of the two numbers on top of the dice is $9$ ?

Problem set 13

Heather, Melody and Christiana are blindfolded. They are each offered three ribbons of colors red, blue and green. What is the probability that they pick three different colors?
In the previous problem, what is the probability that Heather picks a color different from what Melody and Christiana pick?
There are $15$ boy students and a certain number of girl students in a room. Each student is assigned a number. I have to pick one of the numbers assigned to the students at random (blindfolded), and a student comes out if his or her number gets picked. If the probability that a girl student comes out is $\frac{4}{5}$ , what is the total number of students in the room?
What is the ones’ place of $97^{97} + 103^{103}$ ?
What is the value of $\frac{1000}{999}\times\frac{999}{998}\times\frac{998}{997}\times\frac{997}{996}\times\frac{996}{995}\times\frac{995}{994}\times\frac{994}{993}\times\frac{993}{992}\times\frac{992}{991}\times 991$ ?

Problem set 14

What is the value of $99\times 99 + 99\times 97 + 99\times 95 + \cdots + 99\times 5 + 99\times 3 + 99\times 1$ ?
If $\frac{3\times p\times p \times p}{p+p+p} = 49$ and $p$ is a counting number, what is the value of $p$ ?
What is the ones’ place of $97^{97} \times 103^{103}$ ?
If $0.25$ pomogs make $4$ tomogs and $0.01$ domogs make $2$ pomogs, how many tomogs make a domog?

Problem set 15

Two counting numbers add up to $1001$ . What is the biggest possible number you could get out of multiplying them?
$p, q, r$ and $s$ are four consecutive counting numbers with $p<q<r<s$ . Also, $p, q, r$ and $s$ are divisible by $9, 8, 7$ and $6$ respectively. What is the smallest possible value of $s$ ?
If $x,y$ and $z$ represent digits (not necessarily all different), what is the biggest possible 5-digit number of the form $x1y3z$ that is odd and divisible by $11$ ?
What is the ones’ place of $199^{199} - 299^{300}$ ?
If $m$ and $n$ are natural numbers such that $45 \times 3m \times 48 = 24 \times 5n \times 60$ , what is the smallest number that $m$ can be?